
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ
Fakulta elektrotechniky a informatiky
DIPLOMOVÁ PRÁCE
Téma: Možnosti uplatnění elektráren vltavské kaskády pro krytí zatížení
a dynamické služby v ES ČR
1998 TOMÁŠ OTRADOVEC
P R O H L Á Š E N Í
Prohlašuji, že předloženou diplomovou práci jsem vypracoval sám s konzultační pomocí vedoucího projektu a konzultanta. Použité literární prameny jsou uvedeny v oddíle Literatura.
|
V Brně, dne 10.6.1998 |
||
|
Tomáš Otradovec |

OBSAH
1. Význam a úloha AVE v elektrizační soustavě *
2. Historický vývoj vltavské kaskády *
3. Technická a provozní data elektráren vltavské kaskády v současnosti
*3.1 Lipno I *
3.2 Lipno II *
3.3 Hněvkovice
*3.4 Kořensko
*3.5 Orlík *
3.6 Kamýk *
3.7 Slapy *
3.8 Štěchovice
*3.9 Vrané *
3.10 Modřany
*3.11 Štvanice *
4. Teoretický rozbor možných metod řešení *
4.1 Vodohospodářské řešení vodní elektrárny s denním regulováním
*4.1.1 Regulace podle diagramu denního zatížení
*4.1.2 Regulace při denní nepřerušené špičce *
4.1.3 Regulace při omezeném užitkovém objemu nádrže
*4.1.4 Regulace při denní přerušené špičce
*4.1.5 Výroba elektrické energie *
4.2 Využití naměřených závislostí při plánováni provozu
*5. Interpolace *
5.1 Interpolace jako speciální případ aproximace funkce
*5.2 Interpolace algebraickými polynomy *
5.2.1 Existence a jednoznačnost
*5.2.2 Odhad chyby *
6. Zvolení metody řešení
*7. Program Vltava *
7.1 Popis programu *
7.2 Popis algoritmu *
7.2.1 Zpracování vstupních dat *
7.2.2 Zpracování výstupních dat *
7.2.3 Určení výkonu *
7.2.4 Rozdělování průtoku na turbíny
*7.2.5 Ošetření překročení minimálního objemu
*7.2.6 Ošetření překročení maximálního objemu
*7.2.7 Sekundární regulace Orlíku *
8. Demonstrační příklady
*8.1 Pokrývání denního diagramu zatížení
*8.2 Vztah přehrad Orlík - Kamýk
*8.3 Regulační schopnosti vltavské kaskády
*8.3.1 Optimalizace poměrů na nejlepší možnost regulace
*8.3.2 Pokrývání špiček DDZ pomocí vltavské kaskády
*8.4 Dynamické služby
*9. Závěr
*10. Literatura: *
11. Seznam použitých symbolů a zkratek
*12. Přílohy
*Špičková vodní elektrárna je charakteristická tím, že má k dispozici akumulační nádrž. Bývá vybudována při přehradě s akumulačním prostorem jako říční nebo derivační, a proto může využívat zásob vody k regulaci odběru Q na turbíny a podle potřeby výkonu v síti dodat vysoký špičkový výkon. Špičková elektrárna pracuje v době špičkového zatížení, tj. jen několik hodin denně. Má tedy přerušovaný provoz. Vzhledem k tomu, že pracuje pouze ve špič
kách a čerpá vodu z akumulační nádrže, má možnost si i v suchých obdobích zajistit velký průtok na turbínu. Rovněž spád mívá špičková elektrárna vysoký nebo alespoň střední.Protože její špičkový - přerušovaný provoz by způsobil v řece pod elektrárnou velké odtokové potíže různým hospodářským a veřejným zájmům, musí být pod elektrárnou vybudována vyrovnávací nádrž, která má zajistit v řece plynulý průtokový režim, spíše vyrovnanější, než jaký byl v řece před výstavbou špičkové elektrárny.
Z hlediska možností využití hydroenergetického potenciálu vodních toků nemá naše země příliš vhodné podmínky, protože velké řeky na našem území většinou pramení a větší část vodní energie je rozptýlena v malých tocích. Údaje o hydroenergetickém potenciálu našich toků jsou
uvedeny ve Státním vodohospodářském plánu ČSR z roku 1954, ve Směrných vodohospodářských plánech ČSR z roku 1976 a v navazujících publikacích. Technicky využitelný hydroenergetický potenciál byl podle publikace SVP z roku 1989 (v předchozích vydání byl uváděn vyšší) pro Českou republiku stanoven na 3364 Gwh/rok. Stanovení technicky využitelného hydroenergetického potenciálu není jednoznačné. V ČR jako velmi zalidněné zemi naráží jeho využití na značné těžkosti, protože budování velkých nádrží vyžaduje složité zásahy do dnešní struktury území (přeložky silnic a železnic, přemístění sídlišť, průmyslových objektů apod.) a v mnohých případech se velmi obtížně slaďuje s požadavky na ochranu životního prostředí.Přes všechny tyto těžkosti se počítá v budoucnu s, pokud možno, úplným využitím potenciálu řek Vltavy, Labe a Berounky, i s výstavbou několika stovek malých vodních elektráren. Dosavadní nízké využití technického potenciálu vodních toků v ČR, které činí asi 36
%, se má v nejbližších letech rapidně zvýšit.České energetické závody disponují velkými vodními elektrárnami o výkonu nad 10 tisíc kW a malými vodními elektrárnami s výkonem od 10 kW do 10 tisíc kW. Většina malých vodních elektráren zpracovává okamžitý průtok v řece. Jejich výkon je přímo závislý na
hydrologických podmínkách. Větší část velkých vodních elektráren je napájena z akumulačních nádrží, které vznikají umělým přehrazením vodního toku nejlépe v úzkém místě hlubokého údolí. Výkon elektráren napájených z akumulačních nádrží není přímo závislý na okamžitém hydrologickém stavu a lze je proto výhodně použít jako velmi rychlý regulační a zálohový zdroj v elektrizační soustavě. Speciální kategorií jsou přečerpávací vodní elektrárny, které využívají přebytky elektrické energie k načerpání vody do horní nádrže. Načerpanou vodu pak využívají k výrobě špičkové elektrické energie.
Již od nepaměti nalézal člověk kolem řeky Vltavy prostředky ke svému životu a rozvoji společnosti. Počátky spojení života a práce člověka s řekou nalézáme v období těžby dřeva a plavení vorů.
Zásadní obrat ve využití velké vodní energie Vltavy spadá do 19. století. V této době se již objevují návrhy na vodní díla, která mají spoutat energii divoké Vltavy a přinutit ji sloužit člověku. Avšak technické a hlavně ekonomické poměry umožnily první pokus až v roce 1930 - stavbou vodního díla s vodní elektrárnou ve Vraném.
I když v této době pracovalo na území republiky přes deset tisíc malých vodních elektráren místního významu, teprve energetické dílo ve Vraném znamenalo začátek využívání energie Vltavy.
V této době se již mnoho inženýrů vodohospodářů zabývalo návrhy přehrad s vodními elektrárnami, které na sebe postupně navazují. Zrodily se první plány takzvané “Vltavské kaskády”.
Připravovaný projekt doznal pouze zahájení výstavby dalšího stupně v roce 1938 - vodní dílo s elektrárnou vë Štěchovicích.
Začala 2. Světová válka. Válečná léta 1939 až 1945, především násilná fašistická okupace země, znamenala nejen úplné ochromení politického života, ale i nezměrné ztráty na lidských životech a škody hospodářské. V této těžké době se stavělo druhé vodní dílo - Štěchovice. Přesto se našim dělníkům a technikům podařilo vybudovat nejen dobré dílo, ale i prodloužit stavbu především druhé přečerpávací elektrárny tak, aby začala sloužit až svobodnému Československu.
Významným mezníkem ve výstavbě vltavské kaskády se stal únor 1948
; znárodnění klíčového průmyslu a položení základů výstavbě hospodářství řízeného státním plánem zrychlilo tempo výstavby a s ním stoupají i nároky na výrobu elektrické energie.V této době dochází k přehodnocení původních plánů výstavby vodních děl na Vltavě. Z původních více malých stupňů se prosazuje koncepce takzvaných vysokých stupňů na Vltavě. Realizace tohoto plánu začíná v roce 1949 stavbou vodního díla Slapy. V době uvedení do provozu (1954-1955) představuje vodní elektrárna Slapy významný zdroj špičkové energie a z technického hlediska se řadí mezi unikáty své doby.
V roce 1951 byla zahájena další stavba mimořádného významu. Jednalo se o vybudování velkého jezera na Šumavě, které má mimořádný význam energetický i vodohospodářský. V roce 1960 začala pracovat vodní elektrárna Lipno.
V průběhu výstavby vodního díla Lipno byla zahájena výstavba v té době největší přehrady a elektrárny v ČSSR. Přehradní hráz vodního díla Orlík vytvořila na Vltavě umělé jezero dlouhé téměř 70 kilometrů.
Výstavba díla Kamýk probíhala současně (1957 - 1961) s výstavbou Orlíka. Je v podstatě vyrovnávacím stupněm vodního díla Orlík.
V roce 1992 byla uvedena do provozu průtočná vodní elektrárna Kořensko a akumulační vodní elektrárna Hněvkovice. Jejich hlavním úkolem mělo být regulování vodního režimu jaderné elektrárny Temelín.
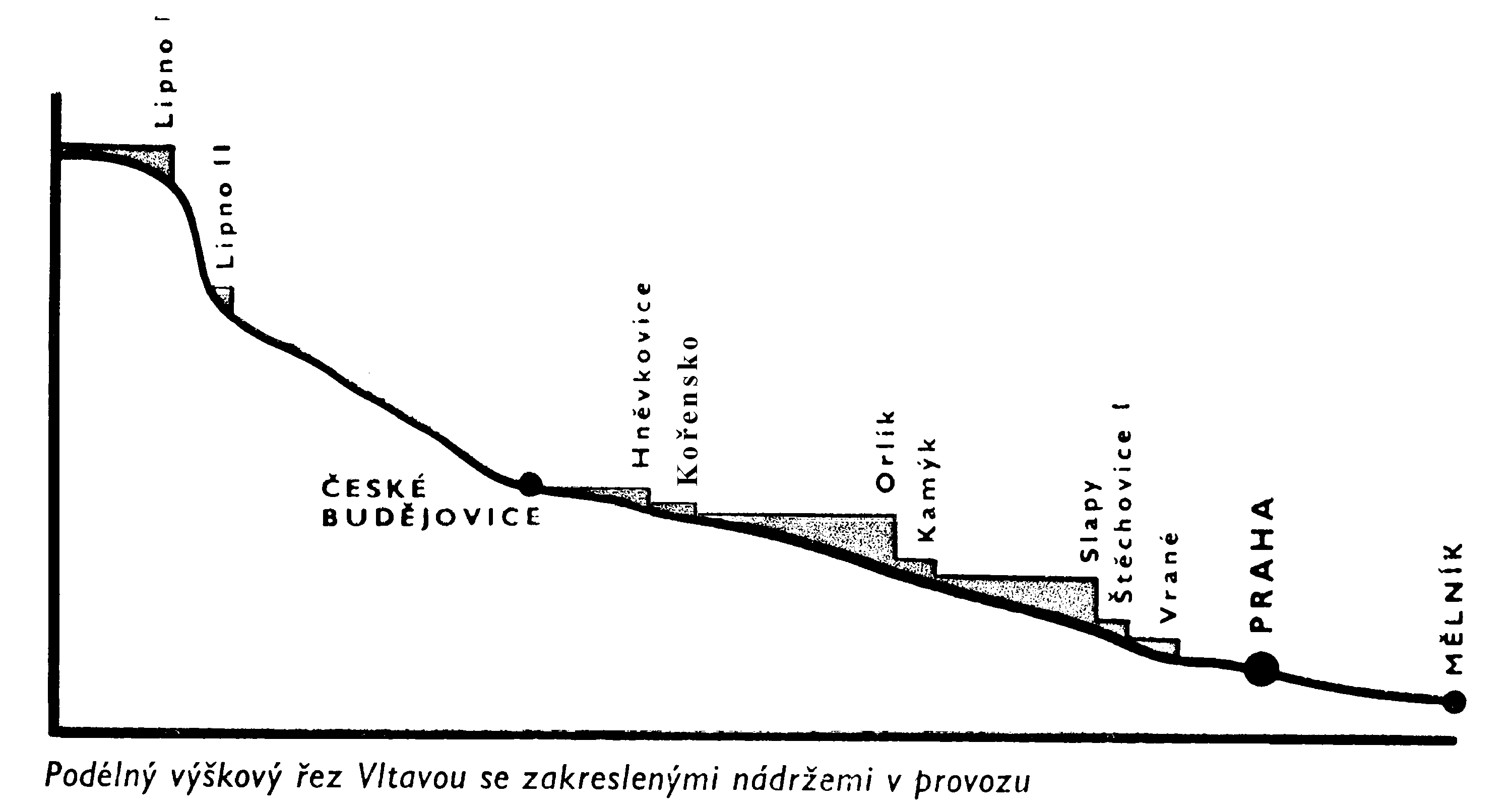
Divize Vodní elektrárny, společnosti ČEZ a.s. organizačně připravuje komplex celkem 10ti vodních elektráren s celkovým instalovaným výkonem 1178 MW, který umožňuje roční výrobu 2 miliard KWh převážně špičkové elektrické energie.
|
spád |
m |
162-148 |
|
počet soustrojí |
2 |
|
|
výkon |
MW |
2 x 60 |
|
průtok turbínou |
m3/s |
46 |
|
typ turbíny |
Francis |
|
|
druh provozu |
turbínový, kompenzační |
|
|
rok zahájení provozu |
1959 |
Lipno I - hráz je kombinovaná zemní a gravitační o výšce 26 m. VE, která je osazena dvěma jednotkami s Francisovými turbínami pro spád 162 - 148 m s celkovým instalovaným výkonem 120 MWe od roku 1959, je umístěna v podzemní kaverně vylámané v hloubce 200 m pod terénem. Voda z VE se odvádí 3,5 km dlouhým odpadním tunelem o průřezu 8,4 x 7,8 m.VE Lipno I vyrobila do konce roku 1992 17,2 PJ (4.782,6 GWh) elektřiny.
|
spád |
m |
10-4 |
|
počet soustrojí |
1 |
|
|
výkon |
MW |
1,5 |
|
průtok turbínou |
m3/s |
20 |
|
typ turbíny |
Kaplan |
|
|
druh provozu |
turbínový |
|
|
rok zahájení provozu |
1957 |
Lipno II - vedena jako průtočná malá vodní elektrárna (MVE) s jedním Kaplanovým turbogenerátorem pro spád 10 - 4 m o výkonu 1,5 MWe od roku 1957. Kombinovaná hráz nádrže je vysoká 11,5 m. Vodní elektrárna Lipno II je plně automatizovaná, bezobslužná, dálkově ovládaná z dispečinku ve Štěchovicích a z elektrárny Lipno I. Hlavní energetický význam, mimo trvalé výroby z vyrovnaného průtoku, je umožnit špičkový provoz elektrárně Lipno I. Do konce roku 1992 vyrobila 585 TJ (162,5 GWh) elektřiny.

|
spád |
m |
14,8-9,3 |
|
počet soustrojí |
2 |
|
|
Výkon |
MW |
2 x 4,72 |
|
průtok turbínou |
m3/s |
30 |
|
typ turbíny |
Kaplan |
|
|
druh provozu |
turbínový |
|
|
rok zahájení provozu |
1992 |
Hněvkovice
- Vodní elektrárna Hněvkovice byla postavena v souvislosti s výstavbou nedaleké jaderné elektrárny Temelín. MVE má dvě Kaplanovy turbíny pro spád 14,8 - 9,3 m o celkovém výkonu 9,44 MWe. Voda je zadržena betonovou gravitační hrází o výšce 16,5 m. V hrázi jsou zabudovány tři přelivy po dvanácti metrech, hrazené ocelovými segmenty s elektropohonem, spodní základová výpust a stavební část plavební komory o rozměrech 45 x 6 m a hloubce 3 m pro lodě o nosnosti do 300 t. Elektrická energie z generátorů je vyvedena přímo do rozvodny čerpací stanice JE Temelín.V provozu od roku 1992.
|
spád |
m |
6,2-2,0 |
|
počet soustrojí |
2 |
|
|
Výkon |
MW |
2 x 1,9 |
|
průtok turbínou |
m3/s |
35 |
|
typ turbíny |
přímoproudá |
|
|
druh provozu |
turbínový |
|
|
rok zahájení provozu |
1992 |
Kořensko
- stejně jako předchozí MVE vybudovaná v souvislosti se zamýšleným provozem ETE. Hlavní funkcí vodního díla Kořensko je udržovat stálou hladinu a tím odstranit hygienické a estetické závady v městské aglomeraci Týn nad Vltavou způsobené kolísáním hladiny zdrže Orlík. Elektrárna je průtočná, nízkotlaká, se dvěma přímoproudými turbogenerátory s horizontálními Kaplanovými turbínami o výkonu celkem 3,8 MWe. Do savek MVE jsou zaústěny odpadní vody z JE Temelín, jejichž potenciální energie je využita v další MVE o výkonu 980 kWe.V provozu rovněž od roku 1992.

|
spád |
m |
70,5 |
|
počet soustrojí |
4 |
|
|
výkon |
MW |
4 x 91 |
|
průtok turbínou |
m3/s |
150 |
|
typ turbíny |
Kaplan |
|
|
druh provozu |
Turbínový |
|
|
rok zahájení provozu |
1961-62 |
Orlík - byla vybavena čtyřmi Kaplanovými turbosoustrojími s desetilopatkovými oběžnými koly o průměru 4,6 m pro extrémní spád 72,5 m (světový primát) o celkovém výkonu 364 MWe od roku 1962. Snaha předvést vyspělost československého energetického strojírenství v oboru vodních turbín překračováním mezních parametrů však měla negativní důsledky v nedosažení předpokládaných účinností. Byl proto navržen nový typ turbíny s osmilopatkovým oběžným kolem, který již dosáhl původně projektovaných hodnot. Kromě zvýšení účinnosti byla prokázána schopnost soustrojí dávat při maximálním spádu ještě vyšší výkon - až 112 MWe oproti původním 91 MWe. Při generálních opravách byly všechny čtyři turbíny vyměněny za vylepšený typ (1994). Těleso přehrady je vybaveno třemi přelivy (15 x 8 m) a dvěmi spodními výpustmi o průměru 4000 mm s hltností 2 x 185,5 m3/s. Do konce roku 1992 vyrobila VE Orlík 38 PJ (10,5 TWh) elektřiny.

|
spád |
m |
15,5-12 |
|
počet soustrojí |
4 |
|
|
výkon |
MW |
4 x 10 |
|
průtok turbínou |
m3/s |
90 |
|
typ turbíny |
Kaplan |
|
|
druh provozu |
Turbínový |
|
|
rok zahájení provozu |
1961 |
Kamýk - čtyři turbogenerátory s Kaplanovými turbínami pro spád 15,5 - 12 m mají celkový výkon 40 MWe. VE Kamýk pracuje v pološpičkovém režimu v tandemu s VE Orlík. Přehrada je betonová gravitačního typu o výšce 24,5 m.V provozu od roku 1961. Do konce roku 1992 vyrobila VE Kamýk 7,7 PJ (2,1 TWh) elektřiny.

|
spád |
m |
56-27 |
|
počet soustrojí |
3 |
|
|
výkon |
MW |
3 x 48 |
|
průtok turbínou |
m3/s |
100 |
|
typ turbíny |
Kaplan |
|
|
druh provozu |
turbínový |
|
|
rok zahájení provozu |
1954-55 |
Slapy - První velká stavba Vltavské kaskády po II. světové válce s betonovou gravitační hrází o výšce 65 m. Přehrada umístěná v úzké soutěsce na konci Svatojánských proudů má originální konstrukční řešení. Pod čtyřmi přelivy (15 x 8 m) s kapacitou 3000 m3/s je přímo v tělese hráze umístěna strojovna elektrárny, veškeré pomocné provozy, administrativní místnosti, unikátní vnitřní rozvodna 110 kV, rozvodna 22 kV, potřebné transformátory a dvě základové výpusti s hltností 2 x 180 m3/s. Elektrárna je vybavena třemi soustrojími s Kaplanovými turbínami pro spád max. 56 m (min. 27 m) o výkonu celkem 144 MWe od roku 1955. Od té doby do roku 1992 vyrobila 39 PJ (10,8 TWh) elektřiny.
|
spád |
m |
20-14,5 |
|
počet soustrojí |
2 |
|
|
výkon |
MW |
2 x 11,25 |
|
průtok turbínou |
m3/s |
75 |
|
typ turbíny |
Kaplan |
|
|
druh provozu |
turbínový |
|
|
rok zahájení provozu |
1943-44 |
Štěchovice I
- dvě Kaplanovy turbíny mají výkon celkem 22,5 MWe. Přehrada je betonová s žulovým obkladem o výšce 22,5 m.V budově elektrárny byla umístěna i dvě soustrojí přečerpávací vodní elektrárny Štěchovice II, která byla v roce 1991 pro fyzické opotřebení odstavena a v současné době probíhá její modernizace výstavbou jednoho nového soustrojí. V provozu od roku 1944. Do konce roku 1992 vyrobila 14,2 PJ (3,96 TWh) elektřiny.Štěchovice II - s instalovaným výkonem 45 MWe (Francisova reversní rychloběžná turbína pro maximální spád 219,5 m, účinnost přečerpávacího cyklu 75,4%, účinnost elektrárny 86%, doba trvání turbínového cyklu 5,13 hodin denně). Uvedena do provozu v srpnu 1995.

|
spád |
m |
10,2-8 |
|
počet soustrojí |
2 |
|
|
výkon |
MW |
2 x 6,94 |
|
průtok turbínou |
m3/s |
90 |
|
typ turbíny |
Kaplan |
|
|
druh provozu |
turbínový |
|
|
rok zahájení provozu |
1936 |
Vrané - stupeň Vltavské kaskády vybudovaný již v roce 1936. Nádrž slouží i jako spodní nádrž pro PVE Štěchovice II. V letech 1978-80 byla provedena modernizace soustrojí - výměna oběžných kol turbín - která zvýšila účinnost a hltnost turbín. V elektrárně jsou instalována dvě Kaplanova turbosoustrojí pro spád 10,2 - 8 m s celkovým výkonem 13,88 MWe. Od zahájení provozu do roku 1992 vyrobila 10,7 PJ (2,98 TWh) elektřiny.
|
spád |
m |
2,25-1,5 |
|
počet soustrojí |
3 |
|
|
výkon |
MW |
3 x 0,5 |
|
průtok turbínou |
m3/s |
30 |
|
typ turbíny |
přímoproudá |
|
|
druh provozu |
turbínový |
|
|
rok zahájení provozu |
1989 |
Modřany
- průtočná MVE se třemi přímoproudými Kaplanovými turbínami pro spád 2,25 - 1,5 m o celkovém výkonu 1,5 MWe, v provozu od roku 1989. Vodu zadržuje jez se čtyřmi poli po 25 metrech, hrazenými ocelovými, hydraulicky ovládanými klapkami. Ve spodní betonové stavbě zakončené rozražeči je provozní chodba, spojující objekty plavební komory s elektrárnou. Výkon turbín je přenášen pryžovými násobnými řemeny na asynchronní motor ve funkci generátoru s napětím 6 kV. Výroba elektřiny do roku 1992 činí 68 TJ (18,9 GWh).|
spád |
m |
4,18-3,23 |
|
počet soustrojí |
3 |
|
|
Výkon |
MW |
3 x 1,89 |
|
průtok turbínou |
m3/s |
55 |
|
typ turbíny |
Přímoproudá |
|
|
druh provozu |
turbínový |
|
|
rok zahájení provozu |
po rekonstrukci 1987 |
Štvanice - poslední MVE vltavské kaskády patřící ČEZ, a.s. se třemi přímoproudými Kaplanovými turbínami pro spád 4,18 - 3,23 m o celkovém výkonu 5,67 MWe. Původní elektrárna byla vybudována již v roce 1914 s výkonem 1,42 MWe (s Francisovou turbínou). Tato VE byla však v roce 1972 odstavena pro úplné opotřebení technologické části. Vtok byl zabetonován, protože se nepočítalo s její obnovou. Teprve po deseti letech byl vypracován projekt na modernizaci. Při náročné přestavbě elektrárny bylo nutno zachovat historickou budovu i charakter ostrova. V provozu od roku 1987. Rekonstruovaná průtočná MVE vyrobila do roku 1992 217 TJ (60,4 GWh) elektřiny.
V některých případech má vodní elektrárna k dispozici určitý omezený akumulační objem vody, který je dán např. přípustným kolísáním hladiny v nádrži nebo zdrži a který lze výhodně využívat ke krátkodobému - dennímu regulování průtoku. Taková vodní elektrárna nemusí pracovat průběžně, ale může sama krýt nebo se podílet na krytí průměrného denního zatížení. Určité oblasti podle jejího diagramu denního zatížení.
Vodní elektrárny s denním regulováním se zpravidla podílejí na krytí středního pásma diagramu denního zatížení, někdy však mohou být využity i pro pokrytí špiček.
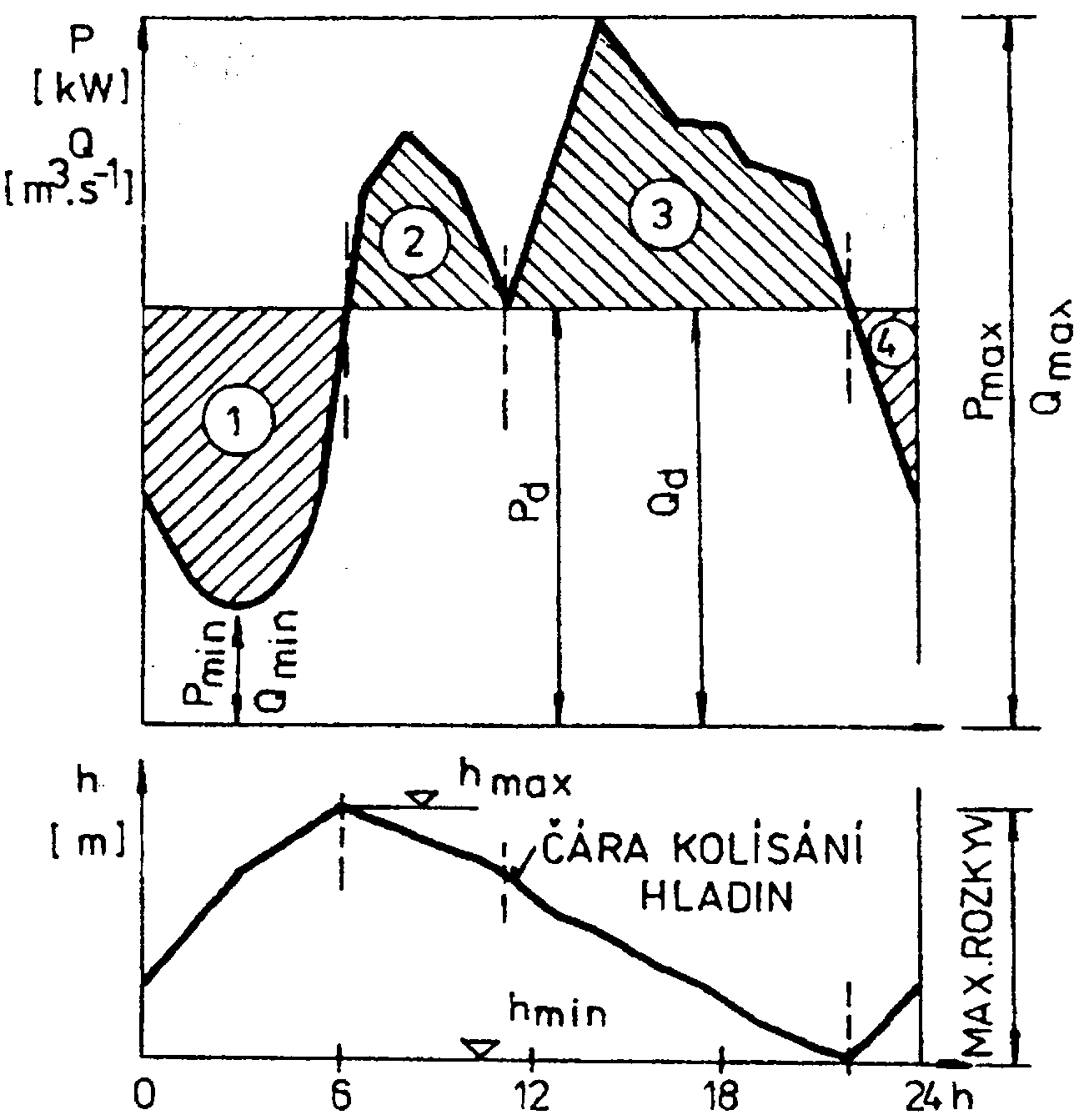 Předpokládejme, že při stálém průtoku řekou pracuje vodní elektrárna s proměnným výkonem, určeným denním kolísáním zatížení
Předpokládejme, že při stálém průtoku řekou pracuje vodní elektrárna s proměnným výkonem, určeným denním kolísáním zatížení ![]() (obr.4-1).
(obr.4-1).
Výkon vodní elektrárny lze určit podle přibližného vzorce
P=9.81*Q*H*![]() [kW] (4.1)
[kW] (4.1)
Kde Q je průtok, H - průměrný spád a ![]() - průměrná účinnost během dne. Potom je výkon přímo úměrný průtoku a zatěžovací křivku lze pokládat i za křivku kolísání průtoků elektrárnou během dne. Střední pořadnice křivky udává střední denní výkon Pd a střední denní průtok Qd.
- průměrná účinnost během dne. Potom je výkon přímo úměrný průtoku a zatěžovací křivku lze pokládat i za křivku kolísání průtoků elektrárnou během dne. Střední pořadnice křivky udává střední denní výkon Pd a střední denní průtok Qd.
Vyšrafované plochy 1 a 4 souhlasí s časem, kdy je průtok Q
d větší než průtok potřebný ke krytí zatížení. Objem vody, vyjádřený plochami 1 a 4, se akumuluje v nádrži a hladina v ní stoupá. Je-li zatížení elektrárny větší než střední výkon Pd, je potřebný průtok turbínami větší než Qd. Doplňující objem vody, vyjádřený vyšrafovanými plochami 2 a 3, se odebírá z nádrže a hladina vody v ní klesá.V nádrži probíhá během 24 hodin úplný cyklus kolísání hladiny - na konci nočního intervalu akumulování vody dosáhne hladina nejvyšší úrovně, během denního intervalu vyšších výkonů klesne hladina do nejnižší polohy. Maximální a minimální průtok, odebíraný v daný den turbínami, se určí z nejvyššího a nejnižšího zatížení pole vztahu
![]() [m3s-1] (4.2)
[m3s-1] (4.2)
Je třeba uvažovat nad počtem spuštěných agregátů v závislosti na typu a hltnosti turbín. Směrodatný je požadavek, aby agregáty pracovaly v celém rozsahu změn průtoků a spádů s dobrou účinností.
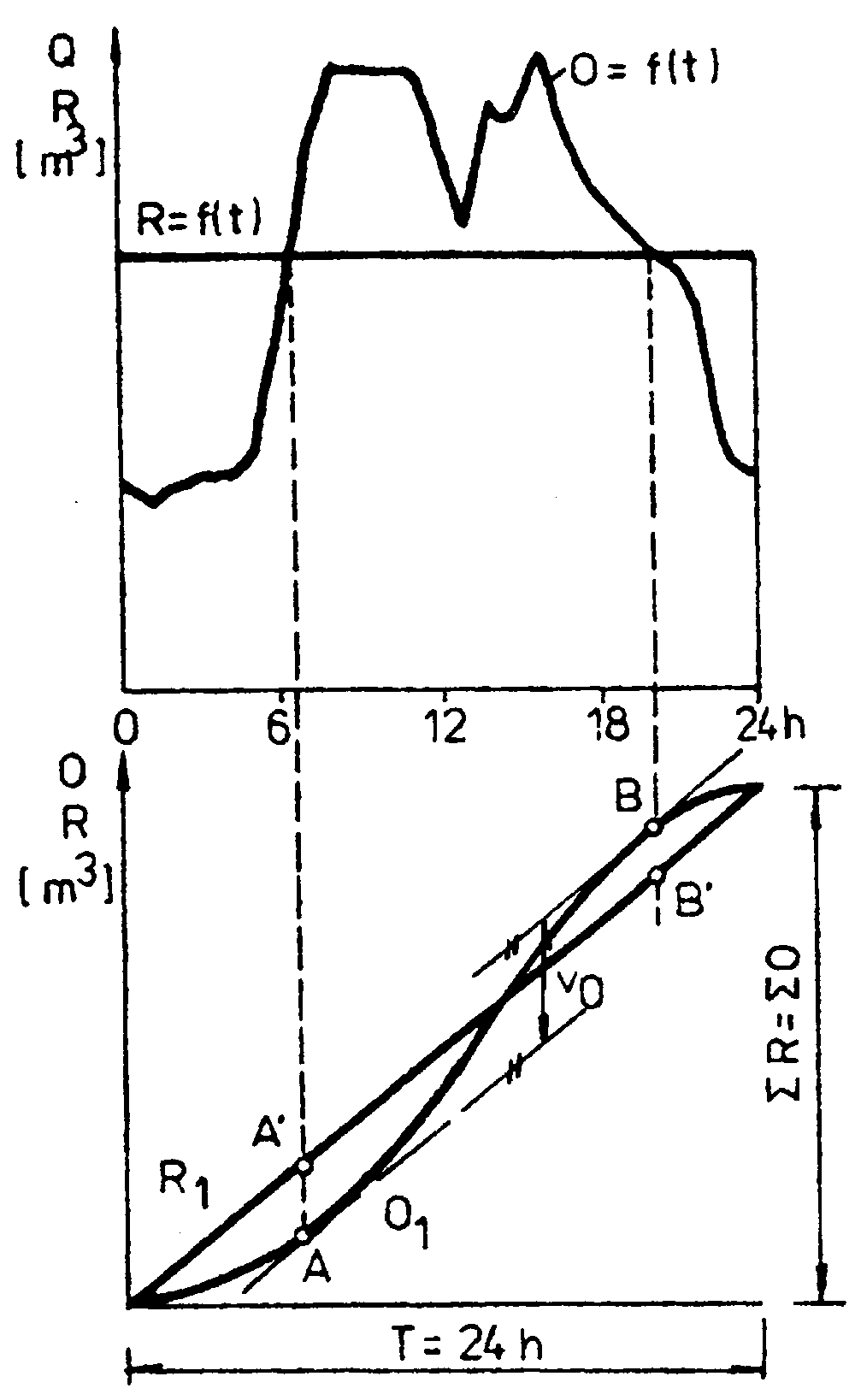
Užitkový obsah nádrže, potřebný pro denní regulaci průtoků, lze zjistit graficky pomocí součtových čar přítoku a odběru, nebo početně. Předpokládejme, že úhrnný celkový denní přítok do nádrže ![]() se rovná úhrnnému dennímu odběru
se rovná úhrnnému dennímu odběru ![]() , takže začátek a konec součtové čáry přítoku R1 a odběru O1 za 24 hodin se bude ztotožňovat (obr.4-2). Součtová čára konstantního přítoku R je znázorněna přímkou R1 a součtová čára proměnného odběru O=f(t) čarou O1. Největší svislá vzdálenost vrcholů A - B součtové čáry odběrů O1, vymezená tečnami rovnoběžnými s přímkou R1, určuje potřebný užitkový obsah Vo nádrže s denním regulováním odtoku.
, takže začátek a konec součtové čáry přítoku R1 a odběru O1 za 24 hodin se bude ztotožňovat (obr.4-2). Součtová čára konstantního přítoku R je znázorněna přímkou R1 a součtová čára proměnného odběru O=f(t) čarou O1. Největší svislá vzdálenost vrcholů A - B součtové čáry odběrů O1, vymezená tečnami rovnoběžnými s přímkou R1, určuje potřebný užitkový obsah Vo nádrže s denním regulováním odtoku.
Uvedené grafické řešení užitkového obsahu, potřebné pro denní regulování odtoku, platí pro vodní elektrárnu, která sama pokrývá proměnné zatížení určité oblasti. Užitkový obsah nádrže vodní elektrárny s denním regulováním, která pracuje ve špičkovém pásmu diagramu denního zatížení, je výhodnější řešit početně. Východiskem k řešení je - obdobně jako u průběžné vodní elektrárny - křivka překročení průtoků. Nejčastější úlohou bývá určit k navržené hltnosti turbín potřebný užitkový objem nádrže, resp. Pro disponibilní užitkový objem nádrže vyšetřit možnosti a hranice špičkového provozu vodní elektrárny.
Tvary špiček diagramu denního zatížení (DDZ) mohou být různé podle toho, jaký je průběh denního zatížení dané oblasti a kterou jeho část má pokrývat regulační vodní elektrárna. Mohou mít tvar lichoběžníka, trojúhelníka nebo zcela obecného obrazce (obr.4-3). Z hlediska denního provozu mohou být nepřerušené nebo přerušené.
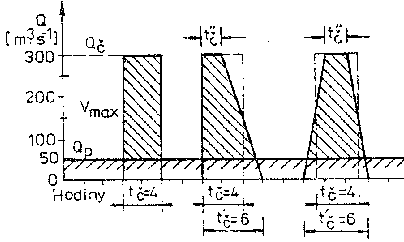 Špičku různého tvaru lze nahradit obdélníkovou o stejné výšce, tj. o stejném výkonu a tím i hltnosti turbín Qč. Podobně místo přítoku vody do nádrže, který ve skutečnosti není ani v průběhu dne konstantní, zavedeme průměrný denní rovnoměrný přítok Qp.
Špičku různého tvaru lze nahradit obdélníkovou o stejné výšce, tj. o stejném výkonu a tím i hltnosti turbín Qč. Podobně místo přítoku vody do nádrže, který ve skutečnosti není ani v průběhu dne konstantní, zavedeme průměrný denní rovnoměrný přítok Qp.
Vyšetříme nejdříve maximální potřebný užitkový objem nádrže pro denní nepřerušenou špičku. Při splnění podmínky, že celodenní rovnoměrný přítok do nádrže se spotřebuje v době trvání obdélníkové špičky, platí
![]() (4.3)
(4.3)
Kde Qp - průměrný denní přítok vody do nádrže, Qč - špičkový odběr rovný hltnosti turbín, tč - délka špičky.
Užitkový objem nádrže se vypočítá z rovnice
V = (24 * Qp - tč * Qp) * 3600 = (24 - tč) * Qp * 3600
[m3] (4.4)
Nebo
V = (tč * Qč - tč * Qp) * 3600 = (Qč - Qp) * tč * 3600
[m3] (4.5)
Po dosazení vztahu (4.3) např. do rovnice (4.4) dostaneme
V = (Qč * tč - Qč* ![]() )*3600 [m3] (4.6)
)*3600 [m3] (4.6)
Maximální užitkový objem nádrže V
max při denním regulování se zjistí z podmínky dV/dtč= 0, z níž dostaneme Qč-2*![]() *Qč=0 (4.7)
*Qč=0 (4.7)
Čili
tč= 12 hodin
A po dosazení z rovnice (4.3)
Qp = ![]() (4.8)
(4.8)
Maximální užitkový objem nádrže V
max bude tedy potřebný pro nepřerušenou denní špičku tč = 12 h při přítoku do nádrže, který se rovná polovině hltnosti turbín vodní elektrárny Qp =Vmax=(24 - 12)* Qp * 3600 = 43200 * Qp (4.9)
nebo
Vmax=(Qč-Qč/2)*12*3600 = 21600 * Qč (4.10)
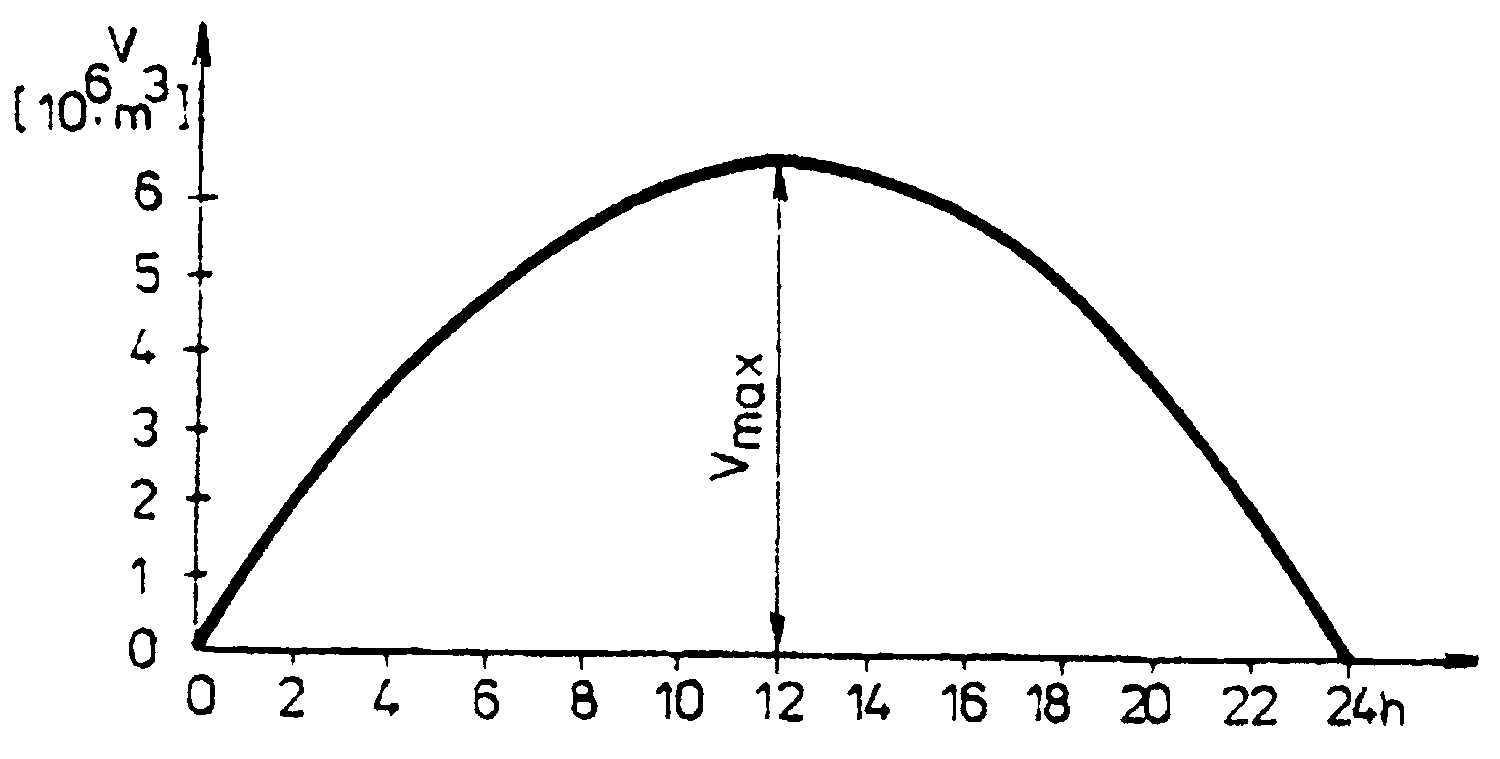
O správnosti tohoto závěru se lze přesvědčit i grafickým znázorněním závislosti (1.4). Dostaneme parabolu, jejíž vrchol (maximum) odpovídá délce špičky tč
= 12 (obr.4-4)Příklad:
Pro ekonomicky odůvodněnou hltnost turbín Qč = 300m3.s-1 a pro minimální zaručený denní přítok do nádrže Qp = 50 m3.s-1 je třeba vyšetřit minimální délku trvání nepřerušené denní špičky a navrhnout užitkový objem nádrže, potřebný na úplné denní regulování.Minimálně zabezpečenému dennímu přítoku Q
p = 50 m3.s-1 odpovídá délka špičky podle rovnice (4.3)
tč = ![]()
Užitkový objem nádrže pro tuto špičku je podle rovnice (4.4)
V50 = (24 - 4) * 50 * 3 600 = 3 600 000 m3
Tento objem však nestačí na úplné denní regulování při vyšších přítocích do nádrže. Při použití nepřerušené špičky je k úplnému dennímu regulování potřebný maximální užitkový objem, odpovídající podle rovnice (4.8) přítoku do nádrže
Qp = ![]() m3s-1
m3s-1
a délce nepřerušené špičk
ytč =![]() h
h
Potřebný užitkový objem nádrže potom podle rovnice (4.4) je
Vmax =(24 - 12)*150*3600 = 6481000 m3
Při zvyšujících se průtocích do nádrže se délky nepřerušených špiček zvětšují a současně se přitom mění potřebný užitkový objem nádrže, jak to ukazují výsledky výpočtu:
Qp = 50 m3.s-1 tč=4 h V50 = 3 600 000
Q = 100 m3.s-1 tč=8 h V100 = 5 760 000
Q = 150 m3.s-1 tč=12 h Vmax= 6 480 000
Q = 200 m3.s-1 tč=16 h V200 = 5 760 000
Q = 250 m3.s-1 tč=20 h V250 = 3 600 000
Je zřejmé, že při přítocích do nádrže Q
p = 300 m3s-1 a větších pracuje vodní elektrárna průběžně, takže není potřebný žádný užitkový objem nádrže - nádrž je plná a průtoky jí procházejí bez regulování.Největší kolísání hladin v nádrži se projeví při regulování denního průtoku Q
p = Qč / 2 = 150 m3.s-1. Při přítocích menších a větších bude hladina v nádrži kolísat méně.Poznamenejme ještě, že při stejných výškách a délkách nepřerušené denní špičky potřebuje největší užitkový objem nádrž, která má regulovat obdélníkové špičky, nejmenší naopak špičky trojúhelníkové. Mezi nimi jsou ostatní tvary špiček. Proto je nejlépe provádět výpočty pro špičky obdélníkové.
Dosud jsme brali v úvahu konstantní hodnotu Qč a pro ni jsme určovali délku špičky tč a potřebný užitkový objem nádrže V při různých denních přítocích Q. V praxi se však může vyskytnout případ, že např. hodnotu Qč je třeba určit se zřetelem k jiným veličinám.
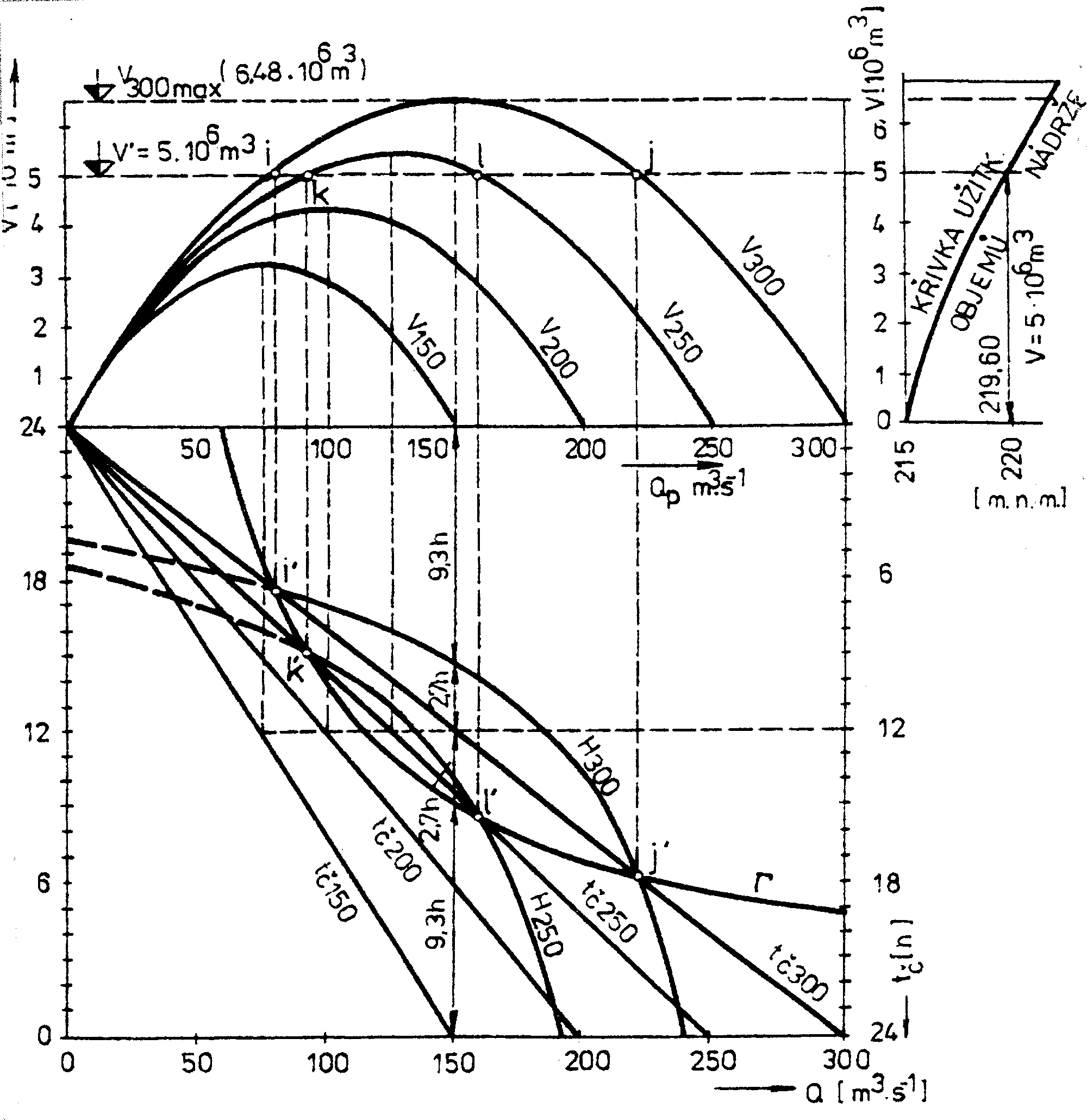
Potom pro zvolenou řadu hodnot Qč nakreslíme svazek parabol Vqč (obr 4-5), které mají společný začátek. Jejich index označuje předpokládanou hltnost turbín vodní elektrárny Qč. Na vodorovné ose je stupnice přítoků a na svislé ose potřebná velikost objemu nádrže V. Rovnice (4.3) udává trvání provozu turbín tč při známém přítoku do nádrže Qp. Pro postupně volené hodnoty Qč lze tuto rovnici graficky zobrazit svazkem paprsků tč, které vycházejí ze začátku souřadnicových os. Z diagramu lze pro určitý denní přítok do nádrže Qp zjistit trvání nepřerušené obdélníkové špičky tč a k tomu potřebnou velikost užitkového objemu nádrže V. Přiřadíme-li ke svislé ose ještě po straně křivku objemů nádrže, můžeme současně určit i příslušné snížení hladiny v nádrži, nebo se přesvědčit, zda její užitkový objem stačí na regulování denních průtoků.
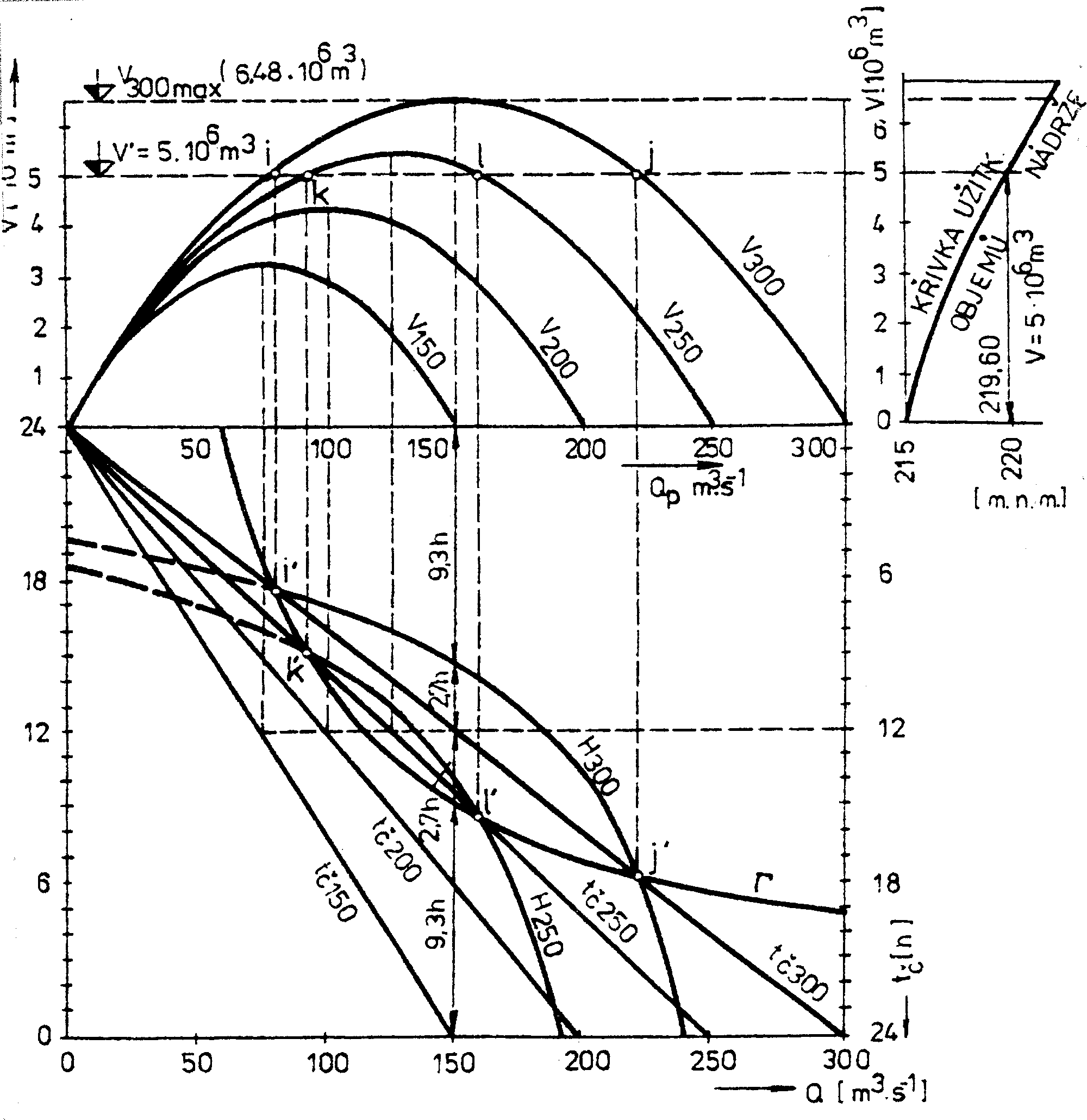 Z diagramu na obr. 4-5 je zřejmé, že největší hodnoty objemů nádrže odpovídají hodnotám Q = Qč/2, tj. dvanáctihodinové nepřerušené obdélníkové špičce. Je-li objem nádrže omezený, z diagramu lehce zjistíme, při kterých hodnotách přítoku do nádrže Qp může ještě vodní elektrárna pracovat s plnou hltností Qč, a po jakou dobu tč popř. na jakou hodnotu je třeba snížit Qč, aby elektrárna mohla pracovat potřebnou dobu tč denně bez přestávky na plný výkon a regulování přítoku aby bylo přitom zajištěno.
Z diagramu na obr. 4-5 je zřejmé, že největší hodnoty objemů nádrže odpovídají hodnotám Q = Qč/2, tj. dvanáctihodinové nepřerušené obdélníkové špičce. Je-li objem nádrže omezený, z diagramu lehce zjistíme, při kterých hodnotách přítoku do nádrže Qp může ještě vodní elektrárna pracovat s plnou hltností Qč, a po jakou dobu tč popř. na jakou hodnotu je třeba snížit Qč, aby elektrárna mohla pracovat potřebnou dobu tč denně bez přestávky na plný výkon a regulování přítoku aby bylo přitom zajištěno.
Často se stává, že topografické nebo jiné místní podmínky dovolují vytvořit nádrž na denní regulování pouze s omezeným užitkovým objemem V´, který je menší než potřebný maximální objem V
max. Potom je třeba zjistit, jaké délce nepřerušené denní špičky a jakému přítoku do nádrže vyhovuje daný omezený užitkový objem nádrže V´. Při špičkovém odběru Qč z nádrže s omezeným objemem V´je možno délku denní nepřerušené špičky vypočítat z rovnicet
č1,2 =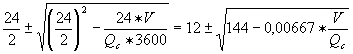 (4.11)
(4.11)
Tato rovnice udává dvě délky denní nepřerušené špičky tč
1 a tč2, které odpovídají dvěma rovnoměrným přítokům do nádržeQp1![]() a Qp2
a Qp2![]() (4.12)
(4.12)
Nádrž s omezeným užitkovým objemem V´ stačí na úplné regulování při nepřerušené obdélníkové špičce o délce tč
< tč1 a tč > tč2, tj. při přítoku do nádrže Qp < Qp1 a Qp > Qp2. Při přítoku do nádrže v mezích Qp1 < Qp < Qp2 nestačí již nádrž regulovat odběr na nepřerušenou denní špičku a je proto třeba upravit provoz vodní elektrárny.V uvedeném rozmezí přítoku do nádrže může vodní elektrárna pracovat:
Vodní elektrárna s denním regulováním odtoku pracuje s přerušenou denní špičkou v případě, když:
Potřebný užitkový objem nádrže pro denní přerušenou špičku je menší než při nepřerušené špičce o objem vody, která přiteče do nádrže v pracovní přestávce mezi oběma částmi denní špičky (obr 4-6), pokud ovšem tento objem není větší než objem první části špičky.
Uvažujme obdélníkové špičky, které trvají tč1 a tč2 hodin a jsou rozděleny denní přestávkou tp1. Po druhé špičce je noční přestávka tp2. Potřebný užitkový objem nádrže (obr. 4-6 - svisle šrafovaná plocha) se vyšetří pomocí vztahu
V´ = (24 - tč1 - tč2 - tp1) * 3 600 * Qp (4.13)
Z tohoto vztahu je zřejmé, že velikost užitkového objemu nádrže závisí - kromě ostatních podmínek - na délce trvání denní pracovní přestávky t
p1 mezi špičkami. Čím delší je tato přestávka, tím menší je potřebný objem nádrže. Délky trvání obou špiček mohou být různé, platí však jednoduché vztahy:tč1 + tč2 = tč (4.14)
tp1 + tp2 = 24 - tč (4.15)
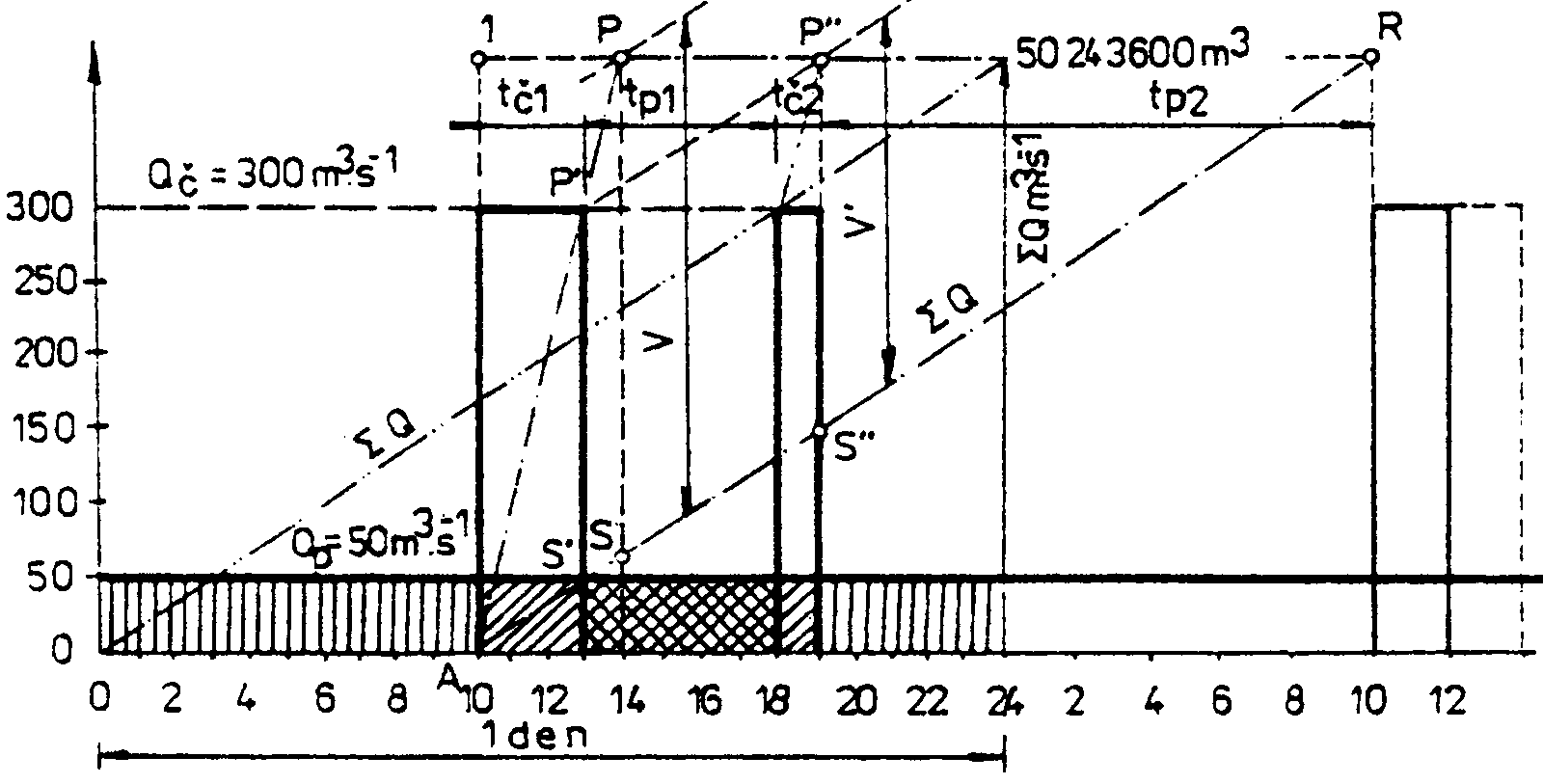
Tento způsob provozu vodní elektrárny je znázorněn na obrázku 4-6. Místo objemu V, potřebného pro regulaci s nepřerušenou špičkou délky tč, postačí při přerušené špičce tč
= tč1 + tč2 menší užitkový objem V´. Z podobnosti trojúhelníků AS´P´ a ASP lze psát úměru:![]()
z níž je
tč1![]() (4.16)
(4.16)
Protože
V = tč * (Qč - Qp) * 3600 (4.17)
je
tč1 ![]() (4.18)
(4.18)
Pro délku druhé špičky dostaneme sloučením rovnic 4.14 a 4.18:
tč![]() (4.19)
(4.19)
Délky nevyhnutných přestávek lze odvodit z podobnosti trojúhelníků R P´´S´´
a R T A:tp2 =![]() (4.20)
(4.20)
tp1 =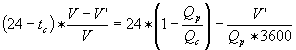 (4.21)
(4.21)
Uveďme nyní názorné graficko-početní řešení případu, kdy je dán omezený užitkový objem nádrže V´. Dosadíme=li do rovnice 4.18 známou hodnotu V´ a za Qč předpokládanou hlt
nost turbín, dostaneme rovnici rovnoosé hyperboly tč = f(Qp), jejíž kladnou větev Hqč zakreslíme do grafu na obr.4-5 (viz. hyperboly H300 a H250 pro hltnosti Qč = 300 a 250 m3s-1). Body i i´, j j´, k k´, l l´ jsou na společných svislicích. Reálný význam mají vypuklé části oblouků nad časovou přímkou mezi body i´j´ nebo k´ l´. Délku první špičky tč1 měříme pro libovolný průtok na příslušné svislici mezi osou Qp a obloukem HQč, pokud je průtok v oboru platné části. Mimo tohoto oboru platí zbývající části časové přímky tčQč .Tak můžeme nakreslit paraboly VQč
všech hltností Qč , které svými vrcholy přesahují hodnotu omezeného objemu nádrže V´. Paraboly, nedosahující svými vrcholy hodnotu V´, příslušejí menším špičkovým hltnostem, pro které postačuje objem nádrže V´ i v případě nepřerušených špiček.Délku druhé špičky tč2 odměříme v pokračování svislice tč1 mezi obloukem HQč a příslušející časovou přímkou tčQč. Pracovní přestávku ( 24 - tč ) je třeba rozdělit na přestávku denní tp1 a noční tp2 , které představují nejkratší mezipřestávky potřebné k tomu, aby bylo možno dosáhnout špiček s trváním tč1 a tč2 tak, aby se nemusely ještě dále rozdělovat.
Když do rovnice 4.20 dosadíme známou hodnotu užitkového objemu V´ pro určitý řešený případ, dostaneme opět hyperbolický vztah mezi proměnnými tp2 a Qp. Kladnou větev této rovnoosé hyperboly ![]() , vypočítanou pro různé průtoky, vyznačíme opět do dolní části diagramu na obr. 4-5. Hyperbola
, vypočítanou pro různé průtoky, vyznačíme opět do dolní části diagramu na obr. 4-5. Hyperbola ![]() platí pro všechny časové přímky tč . Uplatňuje se z ní opět vždy pouze její oblouk vydutý pod příslušející časovou přímkou tč. Hodnota přestávky tp2 měříme na levé svislé stupnici od vodorovné osy Q k hyperbole
platí pro všechny časové přímky tč . Uplatňuje se z ní opět vždy pouze její oblouk vydutý pod příslušející časovou přímkou tč. Hodnota přestávky tp2 měříme na levé svislé stupnici od vodorovné osy Q k hyperbole ![]() . Hodnota přestávky tp2 podle vztahu tp1+ tp2 = 24 - tč .
. Hodnota přestávky tp2 podle vztahu tp1+ tp2 = 24 - tč .
Má-li vodní elektrárna - při daném omezeném objemu nádrže V´- dokonale zvládnout přítoky do nádrže, nesmí překročit zjištěné hodnoty tč1 a tč2 ; může je však zkrátit nebo vzájemně zaměnit. Ani trvání přestávek nemůže elektrárna ze stejných důvodů zkrátit bez toho, že by zkrátila trvání špičkového provozu. Může je však prodloužit nebo časově přemístit v případě, že byly vzájemně přemístěny i špičky tč1 a tč2 . Toto prodlužování a zkracování se však může uskutečnit jen tak, že se zachová platnost vztahů tč1 + tč2 = tč a tp1 + tp2 = 24 - tč .
Tento způsob výpočtu je přibližný. Pokud je však denní kolísání hladin v nádrži malé (do 1 m), jsou výsledky vesměs dostatečně přesné. Přesnější výpočet výroby elektrické energie, z něhož je vidět i časové rozdělení a délky špiček je třeba provést obdobným způsobem jako u vodních elektráren s víceletým regulováním odtoku.
Pro plánování provozu akumulační vodní elektrárny lze použít veličiny naměřené při provozu vodního díla. Musí být známa závislost výkonu na hltnosti a spádu. Mezi výhody této metody patří fakt, že není třeba přepočítávat účinnost přeměny energie na turbíně a generátoru. Ztráty jsou zahrnuty do naměřených veličin. Výsledek potom zcela závisí na přesnosti a úplnosti naměřených dat.
Tato metoda je zvláště vhodná pro algoritmizaci a zpracování na počítači.
Interpolace funkce je jedna z možných metod aproximace reálné funkce. Aproximace funkce obecně spočívá v nahrazení funkce f jinou funkcí g která v nějakém vhodném smyslu napodobuje funkci f a snadno se s ní matematicky pracuje (počítá funkční hodnotu, derivace, integrál). Užití aproximace je různorodé a velmi rozšířené. Již pouhý výpočet funkční hodnoty celé řady funkcí na počítači se provádí pomocí aproximací. Tyto aproximace jsou pro některé funkce zabudovány do výpočetního systému a uživatel si tuto skutečnost ani neuvědomuje.
Z matematické analýzy známe aproximaci funkce f, mající v okolí bodu x0
alespoň n derivací, Taylorovým polynomem n-tého řádu v bodě x
0![]() (5.1)
(5.1)
který splňuje podmínky P
n(x) = g(x) = a0 + a1(x-x0) + … + an(x-x0)n a![]() , j = 0, 1, …, n (5.2)
, j = 0, 1, …, n (5.2)
S využitím této aproximace se setkáváme například při numerickém řešení nelineárních rovnic a v diferenciálních rovnicích. Připomeňme si ještě tvrzení o chybě této aproximace.
Platí:
Nechť funkce
f , f´, … , f(n) existují a jsou spojité v intervalu < a,b > a nechť pro všechna x< a,b > vzorec:
![]() , (5.3)
, (5.3)
kde c je nějaké číslo, které leží mezi x a x
0 a závisí na hodnotě x.Při výběru vhodné aproximace postupuje v numerické matematice tak, že předem zvolíme tvar aproximující funkce jako kombinaci (nejčastěji lineární) základních funkcí z nějaké speciální třídy funkcí. Příklady nejčastěji užívaných základních funkcí:
1, x, …, xn (5.4)
1, ( x-x0 ), ( x-x0 )2,…, ( x-x0 )n , x0 pevné (5.5)
1, cos x, sin x, …, cos Nx, sin Nx, (n = 2N) (5.6)
1, eix, ei2x, …, einx, (i2 = -1) (5.7)
Předpokládejme, že aproximujeme funkci f lineární kombinací základních funkcí g
0, g1, …., gn tj.g(x) = a0 g0 (x) + … + an gn (x) (5.8)
Množinu všech g(x) tvaru (5.8) při pevně zvoleném systému g
0, …,gn označme Vn a nazvěme třída aproximujících funkcí. Úkolem je určit hodnoty parametrů a0, a1, …, an. Označme d(f,g) vzdálenost funkcí f a g. Vyvstává otázka, zda existuje nejlepší aproximace funkce f, tj. taková aproximace g* , že pro všechna gVšimněme si interpolace samostatně, neboť je výchozím bodem pro odvození mnoha metod v jiných oblastech matematiky (numerické derivování, numerická kvadratura, numerické integrování diferenciálních rovnic).
V intervalu I nechť je dáno n + 1 navzájem různých bodů x
0, x1, …, xn, kterým říkáme uzlové body nebo uzly interpolace a dále nechť jsou dány velmi přesně hodnoty y0, y1, …., yn funkčních hodnot f v uzlových bodech, nejlépe yi = f(xi),i = 0, 1, …, n. Máme najít funkci g tak, aby platilo
g(xi) = f(xi), i = 0, 1, …., n (5.9)
K interpolaci nejčastěji používáme funkce
g z prostoru všech algebraických polynomů nejvýše n-tého stupně generovaných 5.4). Označme jej Pn. Je-li f periodická, bývá vhodnější použít trigonometrické polynomy tj. g brát jako lineární kombinaci funkcí (5.6).
Nechť funkce g ![]() Pn . Místo g budeme psát Pn, Pn(x) = a0 + a1x + … anxn, kde aj jsou reálné konstanty. Tato metoda byla v numerické matematice zcela nepostradatelná před rozšířením počítačů neboť se využívala při určování netabelovaných hodnot funkce při vyhledávání v tabulkách. I když toto uplatnění ztratilo význam, zůstává v nezmenšené míře význam interpolace polynomy při odvození dalších numerických metod.
Pn . Místo g budeme psát Pn, Pn(x) = a0 + a1x + … anxn, kde aj jsou reálné konstanty. Tato metoda byla v numerické matematice zcela nepostradatelná před rozšířením počítačů neboť se využívala při určování netabelovaných hodnot funkce při vyhledávání v tabulkách. I když toto uplatnění ztratilo význam, zůstává v nezmenšené míře význam interpolace polynomy při odvození dalších numerických metod.
Platí:
Nechť funkce
f je definována na intervalu I. Potom pro každou množinu navzájem různých bodů x0, x1, … xn ![]() (5.10)
(5.10)
jsou (jediným) řešen
ím soustavy rovnic![]() j = 0, 1, …, n (5.11)
j = 0, 1, …, n (5.11)
Soustava (5.11) je podmínka (5.9) pro konkrétní tvar funkce g. Je to soustava lineárních rovnic pro neznámé a0, a1, …, an, s tzv. Vandermondovou maticí koeficientů. Determinant této matice je pro různé x0, …, xn nenulový, tedy soustava (5.11) má jediné řešení, které bychom takto mohli určit. Koeficienty interpolačního polynomu lze však nalézt jednodušeji, případně hledáme polynom v jiném tvaru. Avšak všechny interpolační polynomy odvozené za podmínek (5.11), proložené stejnými body [xi, yi] , i = 0, …, n , jsou pouze různými tvary téhož polynomu.
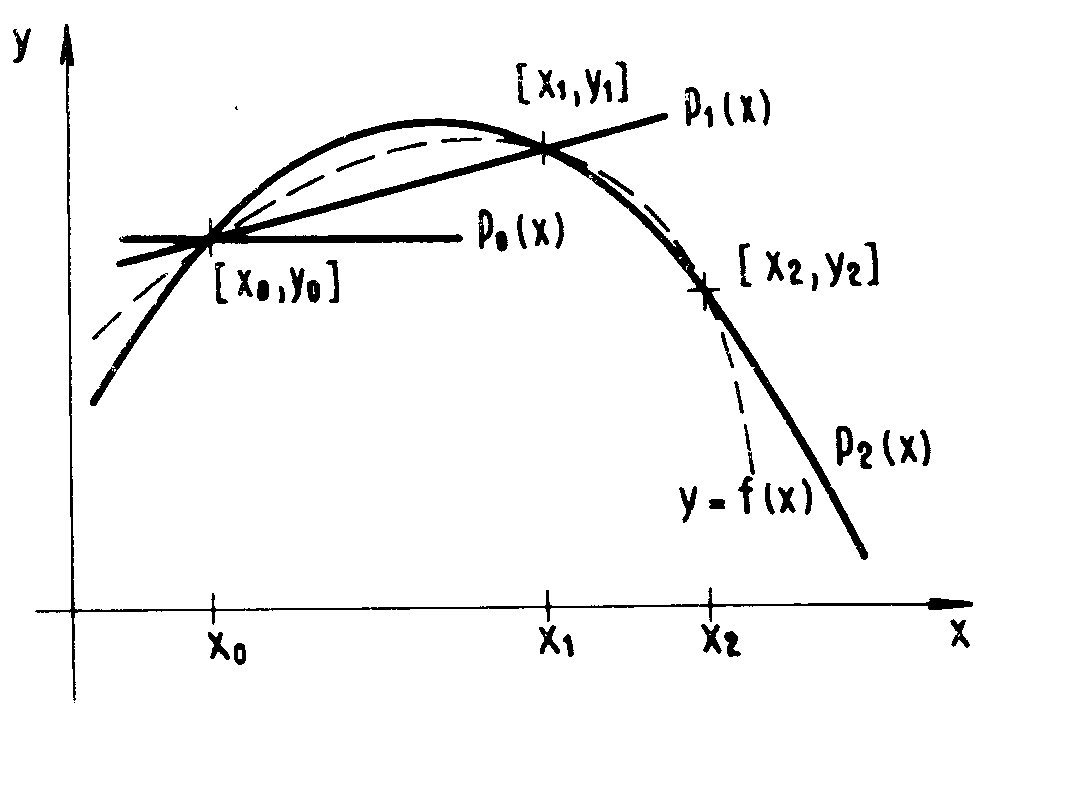 Poznámka: V případě n=1 hovoříme o lineární interpolaci, v případě n=2 o kvadratické interpolaci.
Poznámka: V případě n=1 hovoříme o lineární interpolaci, v případě n=2 o kvadratické interpolaci.
Grafem polynomu P0 je přímka proložená bodem [x0, y0] rovnoběžná s osou x, grafem polynomu P1 přímka procházející body [x0, y0], [x1,y1] a grafem polynomu P2 je parabola s osou rovnoběžnou s osou y a procházející body [x0, y0], [x1, y1], [x2, y2], pokud tyto body neleží na jedné přímce (obr. 5-1).
Nechť interval I obsahuje body x
0, x1, …, xn, a nechť f je (n+1)-krát diferencovatelná funkce na I. Nechť Pn(x) je interpolační polynom n-tého stupně uršený hodnotami funkce f v bodech x0, …, xn. Potom![]() , (5.12)
, (5.12)
kde ![]()
Důkaz
: Z podmínky (5.11) vyplývá, že chyba f(x) - Pn(x) je v uzlech interpolace nulová. Pak pro libovolné x můžeme psátf(x) - Pn(x) = R(x)(x-x0) (x-x1) … (x-xn)
Chceme zdola ohraničit absolutní hodnotu funkce R(x). Položme
![]()
Pak
![]() (5.13)
(5.13)
Platí ![]() , tj. funkce
, tj. funkce ![]() má v intervalu I alespoň (n+2) různých nulových bodů. Z Rollovy věty plyne, že
má v intervalu I alespoň (n+2) různých nulových bodů. Z Rollovy věty plyne, že ![]() má alespoň (n+1) různých nulových bodů (mezi každými dvěma sousedními nulovými body funkce
má alespoň (n+1) různých nulových bodů (mezi každými dvěma sousedními nulovými body funkce ![]() leží alespoň jeden nulový bod funkce
leží alespoň jeden nulový bod funkce ![]() ). Odtud pak postupně dostaneme, že (n+1) derivace funkce
). Odtud pak postupně dostaneme, že (n+1) derivace funkce ![]() má alespoň jeden nulový bod v intervalu I, který označíme c. Je zřejmé, že c leží mezi nejmenším a největším z bodů x0, x1, …, xn.
má alespoň jeden nulový bod v intervalu I, který označíme c. Je zřejmé, že c leží mezi nejmenším a největším z bodů x0, x1, …, xn.
Z platnosti ![]() a rovnice (5.13) plyne
a rovnice (5.13) plyne
![]()
A odtud
![]() c
c![]() I (5.12a)
I (5.12a)
z čehož plyne
![]() , (5.12)
, (5.12)
 kde
kde ![]()
Poznámka:
Po zvážení bylo upuštěno od zahrnutí nádrží Lipno I a Lipno II pro jejich nepřímou souvislost s ostatními elektrárnami vltavské kaskády. Zahrnuty jsou elektrárny Hněvkovice, Kořensko, Orlík, Kamýk, Slapy, Štěchovice a Vrané. Délka uvažovaného úseku Vltavy
je 142 km.Provoz kaskády je algoritmizován a simulován programem VLTAVA vytvořeném v programovacím jazyku Pascal (verze 7) od firmy Borland International
®. Využity byly tabulky sestavené z naměřených závislostí nadmořské výšky hladiny na objemu a tabulky závislosti výkonu na spádu a průtoku přes turbíny. Ukázka tabulek je součástí tištěné přílohy. Kompletní data jsou umístěna na přiložené disketě.Stěžejním bodem této práce bylo vytvoření programu pro simulaci chodu soustavy vodních děl na Vltavě. Využit byl programovací jazyk Pascal. VLTAVA simuluje jeden specifický den kaskády. Na počátku je možno nastavit úroveň zaplnění jednotlivých přehrad a počáteční průtoky.
Den začíná v 0 minut a končí ve 1440 minut. Program načítá ze vstupního souboru požadovaný výkon (z denního diagramu zatížení) a zobrazuje jej na obrazovku. Úkolem uživatele je podle potřeby zadávat výkony jednotlivých elektráren a skládat z nich celkový výkon, který by měl co nejvěrněji kopírovat výkon požadovan
ý po celé kaskádě. Na Orlíku je k dispozici možnost spuštění automatické sekundární regulace, která samočinně reguluje jeho výkon tak, aby doplňoval ostatní elektrárny na požadovaný okamžitý výkon. Program přepočítá podle tabulek zadaný výkon na průtok a ten použije k simulaci průtoků.Během simulace chodu kaskády jsou každých dvacet (modelových) minut do souboru ukládána aktuální výstupní data, která slouží ke zpracování a vyhodnocení simulace chodu vltavské kaskády.
Při prostém běhu programu probíhá cyklus, který v závislosti na změně využitého objemu mění (díky změně spádu) výkon jednotlivých elektráren.
Zpracování vstupních datV souboru se požadovanými okamžitými výkony jsou umístěna data se vzorkováním jedna hodina. Protože program pracuje s krokem jedna minuta, bylo nutné zmenšit krok požadovaného výkonu. Proto bylo opět použitím lineární interpolace mezi každé dvě hodnoty doplněno pět dalších, čímž bylo dosaženo zmenšení kroku požadovaného výkonu na přijatelných deset minut.
Okamžité přítoky do přehrad jsou všechny boční přítoky Vltavy. Nezapočítává se do nich přítok z nadřazené přehrady. Pouze Hněvkovice nemají přímo nad sebou nádrž, proto se započítává Vltava jako přítok do přehrady.
Všechna vstupní data jsou po spuštění programu načtena ze souborů a uložena do dvourozměrných polí.
Zpracování výstupních datBěhem simulace kaskády jsou každých dvacet (modelových) minut do souboru ukládána tato výstupní data:
Výstupní data jsou dále zpracována a slouží k vyhodnocení simulace vltavské kaskády.
V tabulce objemů je nejdříve nalezena příslušná nadmořská výška hladiny, která je použita jako určující hodnota pro vyhledávání výkonu. Protože hodnoty v tabulkách jsou uváděny s určitým krokem, použil jsem pro zvýšení přesnosti lineární interpolaci. Ve ´vyinterpolovaném´ (k aktuální
Průtok je rozdělován na turbíny následovně. Jestliže je dosaženo maximálního průtoku turbíny, přesune se zbývající průtok na další turbínu. Je-li zbývající průtok tak malý, že by na další turbíně nebyl schopen vytvářet uspokojivý výkon, je celkový průtok rozdělen rovnoměrně mezi inkriminované turbíny.
Při změně žádaného výkonu elektrárny proběhne cyklus, který nalezne průtok turbínami zabezpečující požadovaný výkon.
Jestliže dojde k vyprázdnění využitelného objemu elektrárny, všechny její turbíny se zavřou. Je samozřejmě žádoucí se tomuto stavu vyhnout, neboť úplným vypuštěním přehrady se připravujeme o rezervní výkon - nehledě na vliv nadměrného kolísání hladiny na okolí přehrady.
Překročení využitelného objemu je v programu VLTAVA ošetřeno následovně. Dojde-li u některé z přehrad k překročení využitelného objemu a tato přehrada nepracuje na plný výkon, budou nám nabídnuty dvě možnosti. Můžeme buď zvýšit průtok inkriminované přehrady (program vypočítá doporučený minimální průtok) nebo snížit průtok přes turbíny nadřazené přehrady. Pokud o
všem přehrada, která ´přetéká´, běží na plný výkon (nemůže vypouštět přes turbíny víc), bude nám nabídnuta pouze jediná možnost - snížit výkon nadřazené elektrárny.Orlík je díky své flexibilitě a velkému rozsahu výkonu používán pro přesnou regulaci výkonu. V programu VLTAVA je možné tuto regulaci zapnout a Orlík potom velice přesně kopíruje požadovaný výkon. Je ovšem třeba dbát, aby požadovaný výkon nepřestoupil mez danou dosažitelným výkonem Orlíku.
Demonstrační příkladyDemonstrace funkčnosti modelu vltavské kaskády byla provedena na několika různých příkladech. Formou grafů byly zpracovány jednotlivé akční zásahy během dne a jejich odezvy.
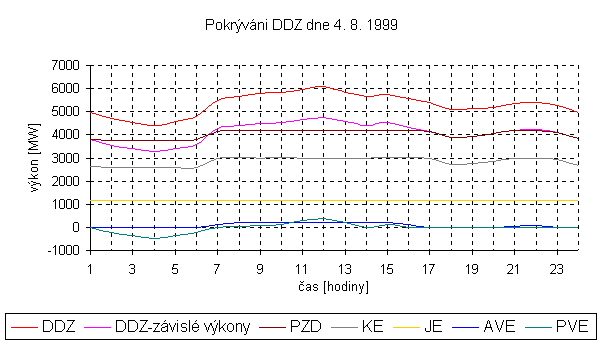
Jako podklad slouží diagram plánovaného pokrývání zatížení dne 4.8.1999. Pomocí programu VLTAVA jsem navrhl optimální režim průtoků přes turbíny elektráren kaskády. Je to jedna z mnoha variant a určitě by bylo možné její vylepšení. Pro demonstraci výsledků programu však vyhovuje.
Uvažované zaplnění využitelného objemu před započetím simulace (hodina 0):
Graf (8-1) znázorňuje uvažované pokrývání denního diagramu zatížení 4.8.1999. Jaderné elektrárny (JE) zásobují ES stálým výkonem. Kondenzační a akumulační vodní elektrárny jsou nasazovány do špičkového provozu. Přečerpávací vodní elektrárny zaručují pokrývání ostrých špiček a využití přebytečné noční energie.
Z denního diagramu zatížení (dále DDZ) je patrné, že požadavek na výkon z kaskády přichází v 6 hodin. Ovšem součástí vltavské kaskády je i průtočná elektrárna Kořensko a elektrárna s minimálním zaručeným odtokem (Vrané - 40 m3/s), takže určitý výkon (řádově několik MW) je dodáván i mimo špičku. V DDZ jsou ovšem zahrnuty pouze akumulační vodní elektrárny. 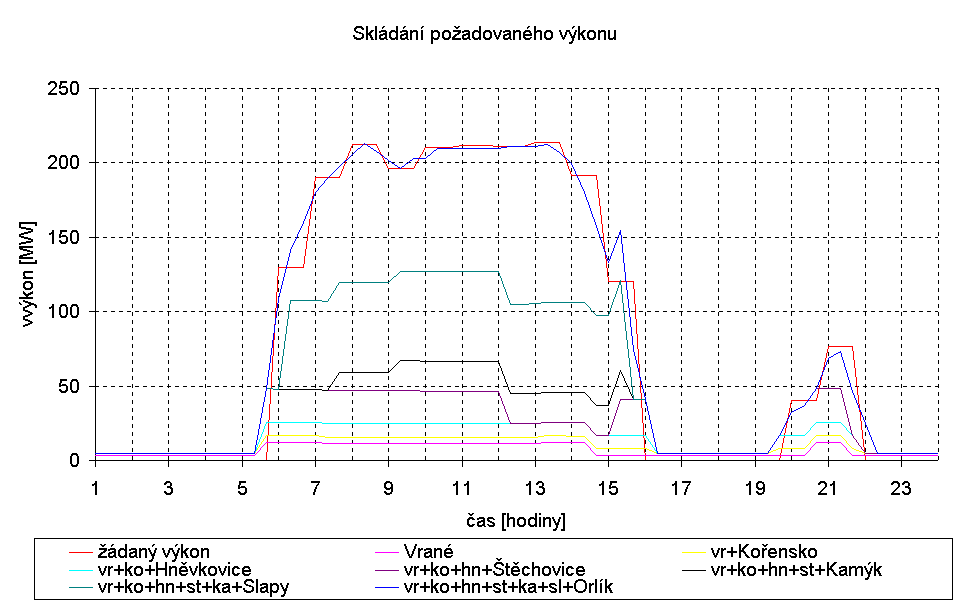
Výkon požadovaný po vltavské kaskádě je složen z dílčích výkonů jednotlivých elektráren. U všech elektráren kromě Orlíka je výkon regulován hrubě (ča
sto pouze 0 nebo 100%). Orlík je pro svou nejlepší regulační schopnost využit pro přesné dorovnání okamžitého výkonu na požadovaný. Pokrytí druhé špičky (po devatenácté hodině) se může zdát poněkud hrubší. Je to způsobeno nevyužitím přesné regulace Orlíkem.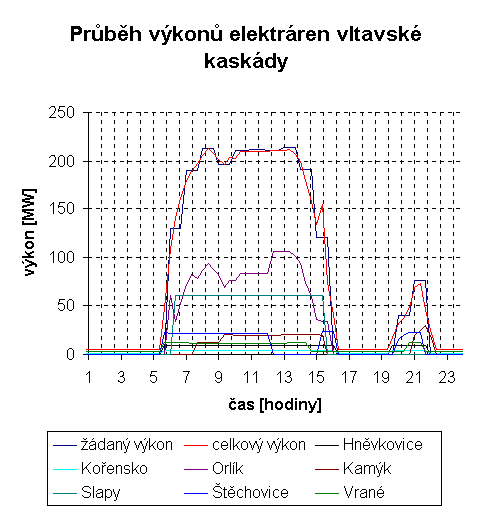
Plánovaného pokrytí bylo až na malé odchylky dosaženo. Největší měrou se podílely elektrárny Orlík a Slapy. (graf 8-3) Ostatní přehrady často plní především funkci vyrovnávání odtoku z těchto "obrů".
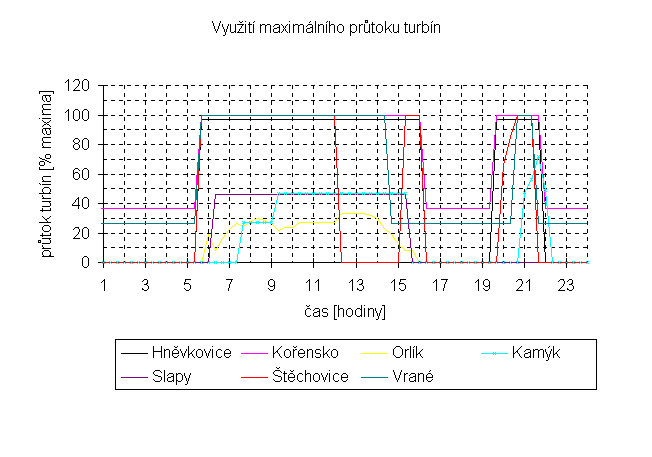
Graf 8-5 znázorňuje využití maximálních průtoků jednotlivých elektráren. Zvláště u Orlíku je patrné nízké využití průtoku. Je způsobeno jednak nutností citlivého přístupu k zaplňováni Kamýku (Vztahu těchto dvou přehrad bude věnována celá kapitola.), ale také faktem, že Orlík je schopen krátkodobě dodávat (při maximálním průtoku) až 360 MW, přičemž špičkový požadavek na celou kaskádu je 210 MW.
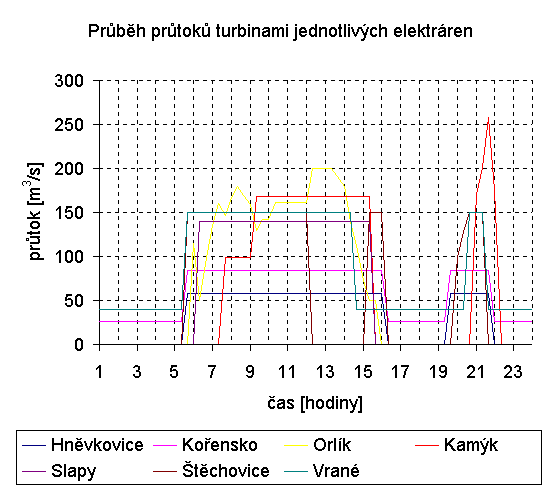
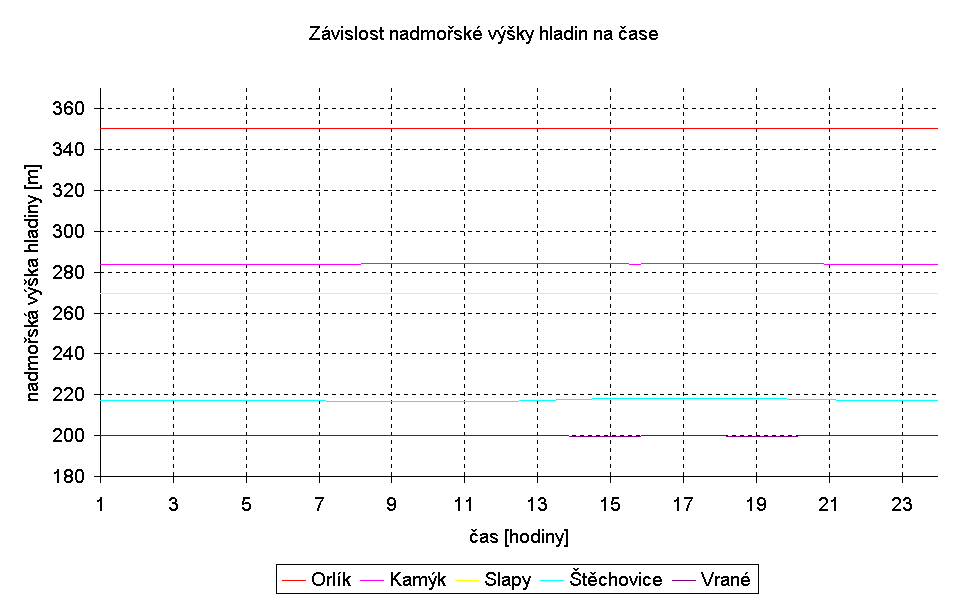
Graf 8-7 zobrazuje především výškové rozdíly hladin. Její změna z něj není příliš patrná. Orlík a Slapy mají podstatně větší vodní plochu než ostatní přehrady, proto je změna hladiny během dne řádově v centimetrech.
Závislost spádu na čase u menších přehrad je znázorněna v grafu 8-4. Největší pohyb vykazuje hladina Kamýku, neboť jeho plocha je oproti např. Orlíku nesrovnatelně menší.
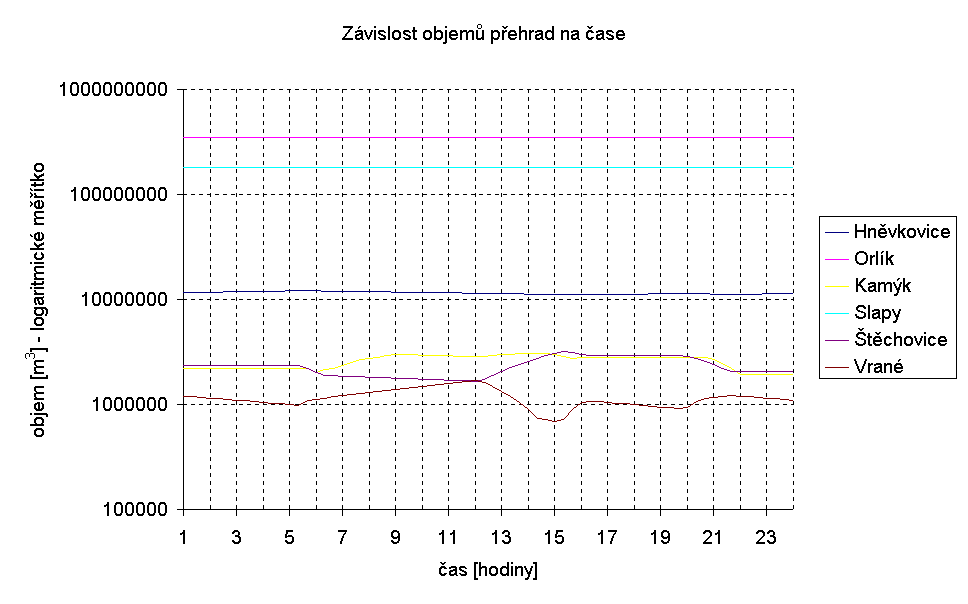
graf -8
Rovněž objemy velkých přehrad (graf 8-8) se nemění natolik, aby to bylo patrné. U menších je změna mnohem výraznější. Dominují Kamýk a Štěchovice.
Zhodnocení
Z výsledků experimentu vyplývá, že rozhodující vliv na výkon vltavské kaskády mají elektrárny Orlík a Slapy. Jejich jmenovitý výkon tvoří více než 80
% celé vltavské kaskády. Tyto dvě přehrady jsou rovněž vhodné pro delší regulační cyklus. Výkon ostatních elektráren je sice menší, ale pro pokrývání DDZ nezanedbatelný. Ať už plánovitě nebo zčásti dílem náhody mají dvě největší přehrady i největší spád, což je samozřejmě výhodné, neboť mohou vysoký výkon dodávat delší časový úsek a omezují je pouze odtokové poměry níže položených přehrad.Nádrž Kamýk byla vybudována s cílem vyrovnávat odtok z turbín Orlíku. Její využitelný objem je "pouze" 4,4 mil. m
Jednoduchým výpočtem zjistíme, že při maximálním průtoku všech turbín obou přehrad dojde k zaplnění Kamýku z nulového využitelného objemu za 5 hodin 6 minut.
![]() (8.1)
(8.1)
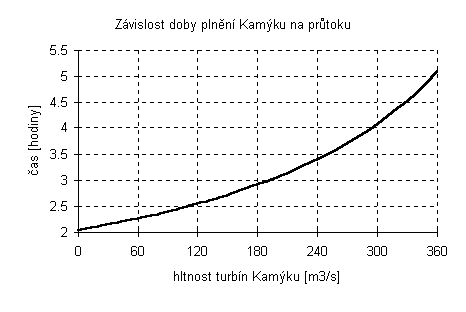
Graf 8-9 zobrazuje dobu, za kterou dojde k zaplnění Kamýku při různém průtoku přes jeho turbíny a maximálním odtoku z Orlíku. Pro špičkové využití Orlíku je volný objem přehrady Kamýk určující, proto je žádoucí mít jej před započetím špičky co možná nejméně zaplněný.
Podobný vztah (ovšem ne tak dramatický) je mezi Slapy a Štěchovicemi.
Uvažujme neplánované odstavení několika bloků přečerpávacích vodních elektráren (Dalešice, Dlouhé Stráně) současně. Za této situace vyvstává potřeba pokrýt ostré špičky DDZ (např. graf 8-12) výkonem z akumulačních vodních elektráren.
Nejlepší možnost regulace poskytují elektrárny Orlík a Slapy. V ideálním případě může být k dispozici regulační výkon až 480 MW. Největšího regulačního rozsahu bude dosaženo, pojedou-li obě elektrárny přibližně na polovinu maximálního výkonu, což vyžaduje dobrou spolupráci s ostatními elektrárnami vltavské kaskády.
Simulace byla provedena tak, aby bez ohledu na DDZ podávaly elektrárny Orlík a Slapy během celého dne polovinu jmenovitého výkonu.
Při simulaci těchto poměrů bylo navrženo toto počáteční zaplnění přehrad:
Ukázalo se, že problém v nedostatečném rezervním objemu není v Kamýku - jeho maximální průtok je více než poloviční oproti maximálnímu průtoku Orlíku - , ale v přehradách zachycujících odpad ze Slap.
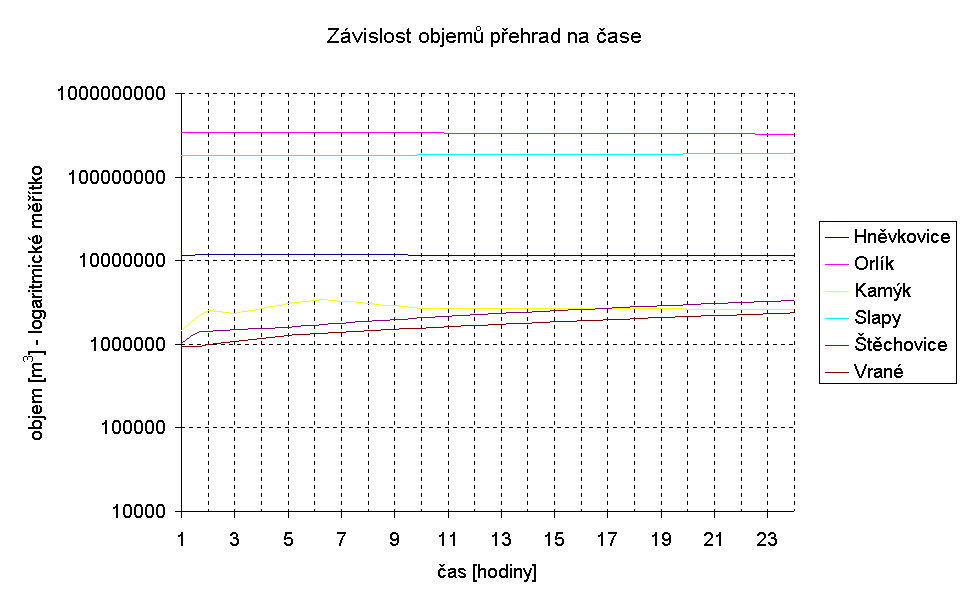
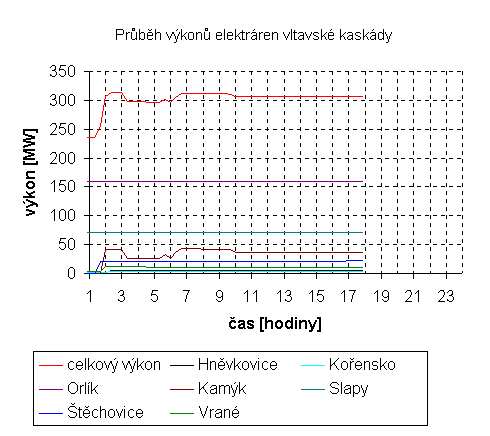
grafy -10 a 8-11
Hltnost turbín Štěchovic a Vraného je 150 m
3/s, což je polovina maxima Slap. Do Vraného ovšem přitéká Sázava s průměrným průtokem 26,1 m3/s a dochází k výraznému plnění přehrady. Rezervní objem Štěchovic a Vraného je však dostatečný, aby situaci zvládl.Došlo-li by k prodloužení tohoto provozního stavu na více než jeden den, nebo by před započetím nebyl v přehradách k dispozici dostatečný objem, bylo by nutno část vody pouštět přes hráz Vraného a tím přij
ít o cennou energii.
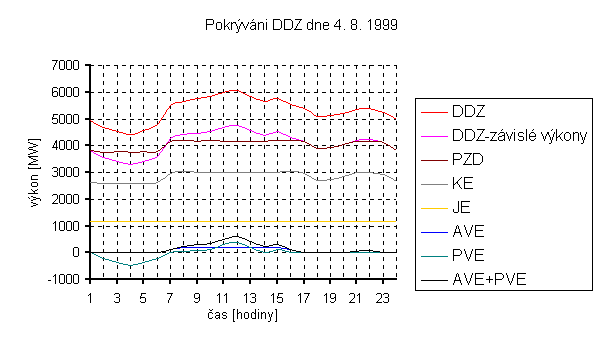 graf -12
graf -12
V grafu 8-12 je vyznačen celkový výkon požadovaný od akumulačních a přečerpávacích vodních elektráren současně. Tento výkon se pokusíme dodat pouze za pomoci vltavské kaskády.
Hodnocení
Výsledky simulace dokazují, že vltavská kaskáda je schopna bez problémů (za cenu velkých výkyvů hladin - viz graf 8-14) dodávat krátkodobě (několik hodin) výkon blízký součtu dosažitelných výkonů jednotlivých elektráren.
Ovšem na pokrytí výkonu přečerpávacích vodních elektráren svým výkonem jednoduše nestačí. V době největšího zatížení bylo potřeba dodat výkon 600 MW, výkon celé vltavské kaskády byl pouze 540 MW. (graf 8-13)
V praxi by nikdy neměla nastat situace, že by v ES nebyla k dispozici žádná PVE. Navíc je možno dovézt špičkovou energii ze zahraničí.
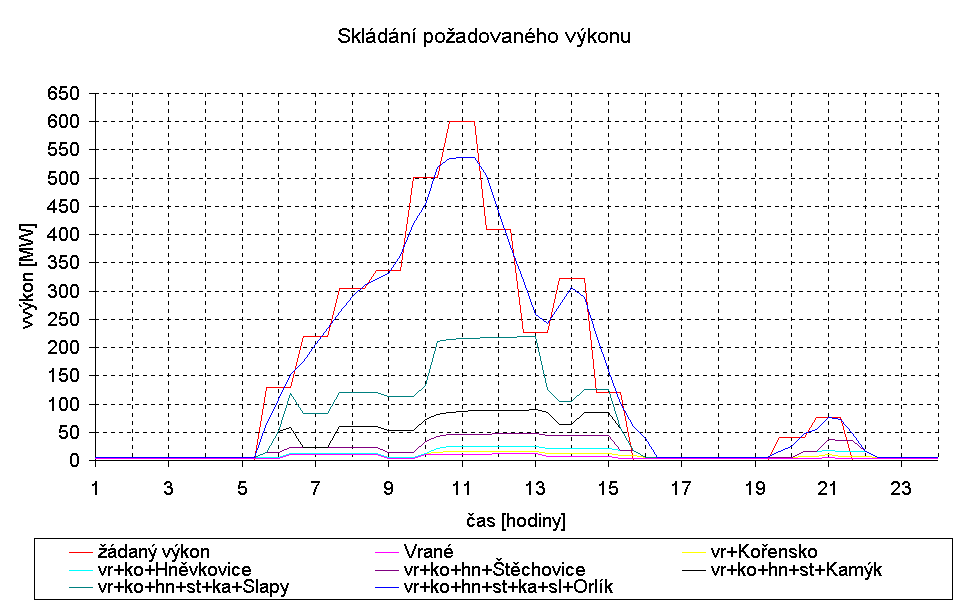 graf -13
graf -13
Při využívání vltavské kaskády pro krytí špiček DDZ nezbývá prostor pro sekundární regulaci - krátkodobé snižování a zvyšování výkonu podle aktuálního zatížení. Proto je nutná účast PVE na pokrývání špiček.
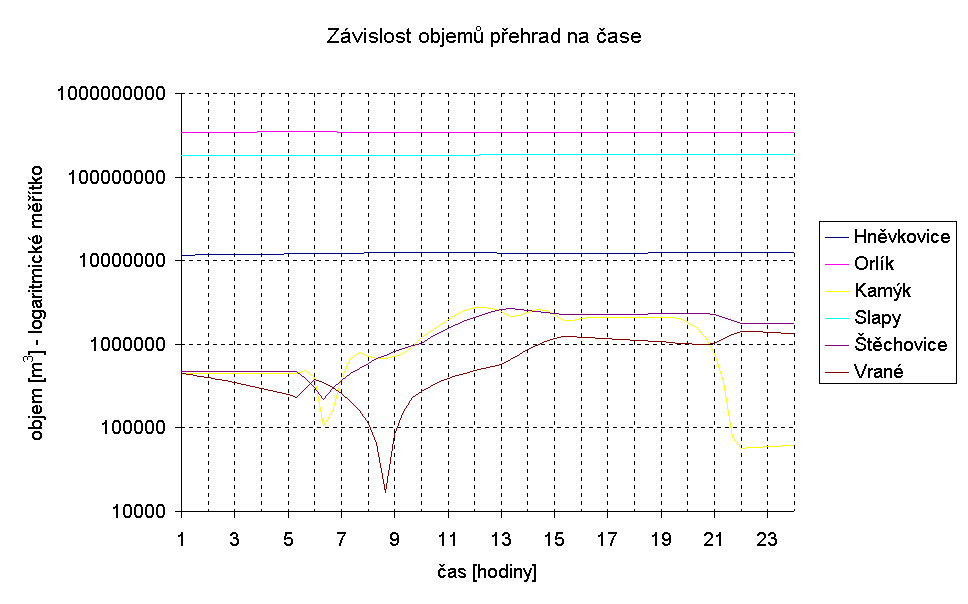
graf -14
Pro zabezpečení dynamických služeb jsou využívány elektrárny Orlík a Slapy. Podávají stabilně střední výkon, od kterého se v případě potřeby odchýlí.
Aby byl záložní výkon k dispozici skutečně ihned, je žádoucí rozdělit střední výkon rovnoměrně mezí turbíny s nižším průtokem než je maximální. Pokud by výkon byl rozdělen mezi turbíny tak, že jejich průtoky by byly blízké maximu, při požadavku výkonu z ES by najížděla další turbína, což představuje u Orlíku zdržení 210 vteřin. Snížení průtoku turbín s sebou přináší pokles účinnosti resp. zvýšení průtoku pro dosažení daného výkonu. (tab 8-1)
|
Turbín v provozu |
Výkon |
Potřebný průtok |
|
2 |
2 x 80 MW |
306 m3/s |
|
3 |
3 x 53,4 MW |
310 m3/s |
|
4 |
4 x 40 MW |
316 m3/s |
Cílem této práce bylo seznámit se s vltavskou kaskádou a jejími možnostmi při krytí zatížení elektrizační soustavy České republiky.
K tomuto účelu jsem si vytvořil program VLTAVA, s jehož pomocí byly modelovány výkony elektráren vltavské kaskády na základě průtoků a výšky hladin jednotlivých přehrad.
Výsledky dokazují, že rozhodující vliv na výkon kaskády mají elektrárny Orlík a Slapy díky svému velkému objemu a hlavně spádu. Ostatní elektrárny plní často především funkci vyrovnávání odtoku.
Navržené pokrývání denního diagramu zatížení splňuje pouze demonstrační účel; v reálném provozu nelze uvažovat jen průtoky a objemy, ale také environmentální a sociálně ekonomický vliv pohybu hladiny přehrad na danou lokalitu. Rovněž je potřeba brát v úvahu manipulační pravidla a dlouhodobý plán využívání vodního díla.
Dalšího zjednodušení jsem se dopustil uvažováním pouze průměrných dlouhodobých průtoků. Průtoky se během roku výrazně mění (rovněž každý rok je jiný) a hodnota dodané energie je závislá především na množství vody, které má kaskáda k disp
ozici.Cíle práce - demonstrovat možnosti využití kaskády - však bylo dosaženo.
P W výkon
Pd W střední denní výkon
f Hz frekvence
Q m3/s průtok
Qd m3/s střední denní průtok
Qc m3/s špičkový odběr
H m spád
h
- účinnosttc s délka odběrové špičky
V m3 objem
Použité zkratky elektráren
hn Hněvkovice
ko Kořensko
or Orlík
ka Kamýk
sl Slapy
st Štěchovice
vr Vrané
programem vltava